지도 학습 스터디 내용 요약
업데이트:
2. 지도 학습
- 요약
- kNN
- 작은 데이터셋일 경우, 기본 모델로 좋고 설명하기 쉬움
- 선형 모델
- 첫 번째로 시도할 알고리즘
- 대용량 데이터셋 가능, 고차원 데이터에 가능
- 나이브 베이즈
- 분류만 가능, 선형보다 빠름
- 대용량 데이터셋, 고차원 데이터에 가능
- 선형 모델보다는 덜 정확
- 결정 트리
- 매우 빠름
- 데이터 스케일 조정 필요 없음
- 시각화하기 좋고, 설명하기 쉬움
- 랜덤 포레스트
- 하나의 결정트리보다 좋은 성능
- 안정적이고 강력
- 데이터 스케일 조정 필요 없음
- 고차원 희소 데이터(텍스트같은)에서는 잘 안맞음
- 그래디언트 부스팅 결정 트리
- 랜덤 포레스트보다 조금 더 좋음
- 하지만 상대적으로 학습 시간 느리나 예측은 빠르고 메모리 조금 사용
- 단, 튜닝을 더 많이 해야함
- 서포트 벡터 머신
- 비슷한 의미의 특성으로 이뤄진 중간 규모 데이터셋에서 잘 사용
- 데이터 스케일 조정 필요
- 매개변수 민감, 튜닝 필요
- 신경망
- 대용량 데이터셋에서 매우 복잡한 모델 만들 수 있음
- 매개변수와 데이터 스케일에 민감
- 큰 모델에서 학습 오래걸림
지도학습
- 입력과 출력 샘플 데이터가 있고, 주어진 입력으로부터 출력을 예측하고자 할 때 사용
분류와 회귀
출력 값에 연속성이 있는지 확인하여 회귀와 분류 문제를 구분할 수 있음(y-회귀, n-분류)
- 분류
- 미리 정의된 클래스 레이블 중 하나를 예측
- 이진 분류(binary classification)
- True/False, 0/1, 양성클래스(positive)/음성클래스(negative)
- 다중 분류 존재(multiclass classification)
- 클래스가 여러개
- 회귀
- 연속적인 숫자 예측
- 부동소수점수(in programming), 실수(in math)
- 연속적인 숫자 예측
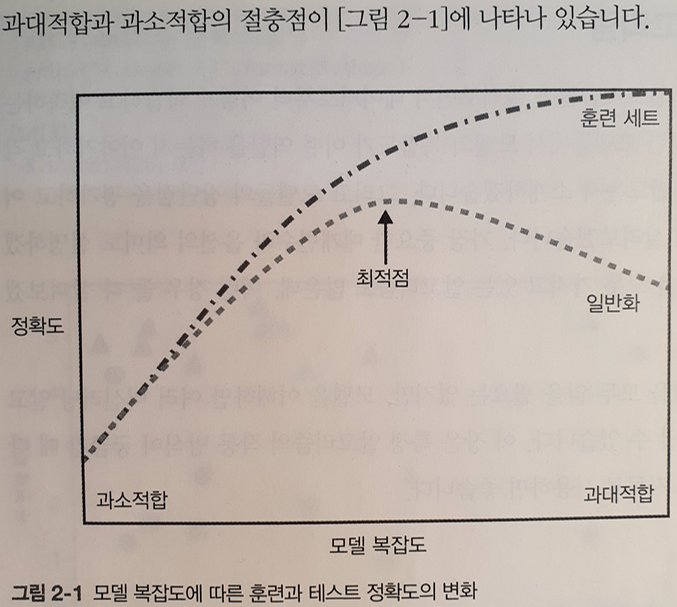
일반화, 과대적합, 과소적합
- 일반화
- 모델이 처음보는 데이터에 대해 정확하게 예측할 수 있으면 일반화되었다 라고 함
- 과대적합(overfitting)
- 가진 정보를 모두 혹은 너무 많이 사용하여 과하게 복잡한 모델을 생성하는 것
- 훈련데이터에 너무 가깝게 맞춰져서, 새로운 데이터에 일반화되기 어려울 때 발생
- 과소적합(underfitting)
- 너무 간단한 모델이 선택되는 것
- 데이터의 본질과 다양성을 놓칠 것이며, 훈련 세트에도 잘 맞지 않을 것
- 훈련 세트와 테스트 세트의 결과가 매우 비슷
- 모델을 복잡하게 할수록 훈련 데이터는 더 정확히 예측하지만, 과하면 각 데이터 포인트에 너무 민감해져서 새로운 데이터에 일반화가 잘 안됨.
-
이 최적점을 만족하는 모델을 만들어야 함
-
모델 복잡도와 데이터셋 크기(레코드 수) 간 관계
- 레코드가 많을수록 과대적합 없이 복잡한 모델 생성 가능
- 하지만, 중복 혹은 비슷한 특성의 레코드가 많은 것은 의미가 없음
- 데이터를 적절하게 많이 얻는 것이 모델 일반화에 큰 도움을 줌
- Q. 그럼 데이터를 얼마나 모을 지 어떻게 정할까? → [검정력, 효과크기, 표본크기, 유의수준]을 통해?
지도 학습 알고리즘
kNN 분류 (k-Nearest Neighbors, k-최근접 이웃 분류)
- 훈련 데이터셋을 저장
- 새로운 데이터는 훈련된 데이터셋에서 어떤 분류에서 가장 가까운지, 최근접 이웃이 누구인지 찾아내어 분류
- 결정 경계 (decision boundary)
- 각 분류를 구분하는 경계
- 이웃 수가 많을수록 경계는 부드러움
- 이웃 수가 적으면 모델의 복잡도는 높아짐
- 이웃 수가 많으면 모델의 복잡도는 낮아짐
- 이웃 수가 데이터 수와 같으면, 최빈값으로 예측됨
- 이웃 수는 모델의 복잡도-일반화에 영향을 끼치므로, 잘 선택해야함
- 몇 개의 이웃 수가 과대, 과소 적합을 피하여 적절한 지 테스트 필요할 듯
- kNN 회귀
- 가장 가까운 이웃 k개의 평균으로 예측
- kNN reg의 score는 R²로 나타남( 0≤R²≤1)
- 분류와 마찬가지로, 이웃 수가 일반화에 크게 영향을 끼침
- 이웃이 적으면, 훈련 데이터는 잘 예측하지만, 불안정한 일반화
- 이웃이 많으면, 훈련 데이터에는 잘 안 맞을 수 있지만, 안정된 예측을 얻을 수 있음
- 매개변수와 장단점
- 데이터 포인트 사이의 거리를 재는 방법
- 책에서는 다루진 않기 때문에 추가적으로 공부 필요
- 기본적으로 여러 환경에서 잘 동작하는 유클리디안 거리 방식 사용 (metric=’minkowski’, p=2 일 때 유클리디안 거리와 같음)
- 이웃 수
- 장점, 특징
- 이해하기가 쉽다.
- 많이 조정하지 않아도 자주 좋은 성능을 발휘
- 더 복잡한 알고리즘을 적용하기 전에 시도해볼 수 있는 시작점
- 데이터 전처리 과정이 중요
- 많은 특성을 가졌거나, 특성 값 대부분이 0인(희소한) 데이터셋과는 잘 작동하지 않음 - 단점
- 샘플 수가 많아지면 예측이 느려짐
- 특성 처리 능력이 부족하여 현업에선 잘 안쓰임
- 데이터 포인트 사이의 거리를 재는 방법
선형 모델
- 선형 함수를 만들어 예측 수행
y^ = w[0] * x[0] + b
- 특성 수에 따라 모델의 모양이 달라짐
- 1: 직선, 2: 평면, 더 높은 차원에선 초평면
선형 회귀 (최소제곱법, OLS)
- 예측과 훈련 세트에 있는 타깃 y 사이의 평균제곱오차(MSE, mean squared error)를 최소화하는 w, b(절편, 기울기)를 찾음
- 매개변수가 없는 것이 장점이지만, 매개변수가 없어서 모델의 복잡도를 제어할 방법도 없다.
- 피처가 적은 데이터 세트에선 모델이 단순하므로 오버피팅의 우려가 적음
- 피처가 많으면 모델이 복잡해짐, 오버피팅됨
릿지 회귀 (Ridge Regression)
- y^ = w * x + b 함수 사용은 동일
- w의 선정 방식이 다름
- 예측 뿐 아니라 추가 제약 조건을 만족시키기 위한 목적도 있음
- 가중치 w의 모든 원소가 0에 가깝게 되도록 절대값을 최소화
- 이러한 제약을 규제(regularization)이라고 함
- 규제? - 과대적합이 되지 않도록 모델을 강제로 제한
- 릿지 회귀에 사용하는 규제 방식은 L2 규제라고 함
- alpha 값을 조정하여 일반화되도록 조정
- 높이면 w계수가 0과 가까워짐
- 훈련세트의 성능은 저하되지만, 일반화에는 도움됨
- 학습 곡선(learning curve)
- 데이터셋 크기에 따른 모델의 성능 변화를 나타낸 그래프
- 데이터가 많아질수록 릿지의 규제는 중요도가 떨어진다. (마치 n이 커지면 불편추정을 위해 n-1로 나누는것이 큰 의미가 없는것처럼)
라쏘 (Lasso)
- 계수를 0에 가깝게 하는 것에선 릿지와 동일
- 실제로 계수가 0이 되는 경우도 있음 (= 모델에서 제외되는 특성도 생김)
- 자동 특성 선택이라고도 볼 수 있음 (특성이 제외되니까)
- 라쏘의 규제는 L1 규제라고 부름
- 릿지와 라쏘
- 보통 릿지를 선호
- 피처를 자동으로 탈락시키지 않기 때문
- 특성이 너무 많고, 그 중 일부분만 중요하다면 라쏘가 더 좋은 선택일 수 있음
- 특성 중 일부만 사용하므로, 쉽게 해석할 수 있는 모델을 만들어줌 (= 분석하기 쉬움)
- Lasso와 Ridge의 페널티를 결합한 ElasticNet도 있음
- 좋은 성능을 내지만, L1, L2 규제를 위한 두 매개변수를 조정해줘야함
- 보통 릿지를 선호
분류용 선형 모델
- 이진 분류
- y^ = w[0]x[0] … +w[p]x[p] + b > 0
- 0보다 크면 1, 작으면 -1로 예측
- 회귀용 선형 모델에서는 y^의 피처가 선형 함수
- 직선, 평면, 초평면
- 분류형 선형 모델에서는 결정 경계
- 이진 선형 분류기는 선, 평면, 초평면을 사용해서 두 개의 클래스를 구분하는 분류기
선형 모델 학습 알고리즘을 구분하는 두 가지 방법
- 특정 계수와 절편의 조합이 훈련 데이터에 얼마나 잘 맞는지 측정
- 규제가 있는지, 있다면 어떤 방식인지
- w, b를 조정하는 것은 불가능
로지스틱 회귀(Logistic Regression), 선형 서포트 벡터 머신(Support Vector Machine)
주의점: 로지스틱 회귀는 회귀 알고리즘이 아닌 분류 알고리즘임!
- 두 모델 모두 릿지와 마찬가지로 L2 규제를 사용 (매개변수 C)
- C값이 높아지면 규제가 감소
- 높은 C값은 훈련세트에 최대한 맞추려함 (= C값이 높아지면 개개의 데이터 포인트를 정확히 분류하려 노력)
- 낮은 C값은 계수 벡터(w)가 0과 가까워짐 (alpha랑 반대네) (= C값이 낮아지면 데이터 포인트 중 다수에 맞추려함)
- C값이 높아지면 규제가 감소
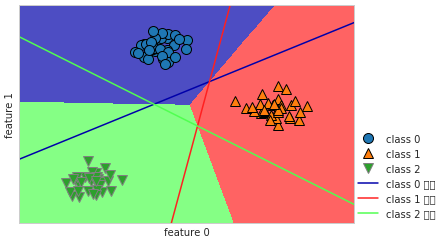
다중 클래스 분류용 선형 모델
- 보통 선형 분류 모델은 이진 분류만을 지원
- 일대다 방법을 통해 다중 클래스 분류로 확장함
- 클래스별 이진 분류기를 만들면, 각 클래스가 계수 벡터(w)와 절편(b)을 하나씩 갖게됨
- w[0]x[0] + … w[p]x[p] + b 결과값이 가장 높은 클래스가 해당 데이터 클래스 레이블로 할당
-
중간에 겹치는 부분(다중 클래스 경계가 모두 나머지로 분류한 부분): 가장 가까운 클래스로 분류
- 선형 모델의 매개변수와 장단점
- 회귀 모델: alpha
- LinearSVC, LogisticRegression: C
- alpha 값이 클 수록, C 값이 작을수록 모델이 단순해짐
- 특히 회귀 모델에서 매개변수 조정이 매우 중요
- alpha, C 모두 로그 스케일로 최적치를 정함 (10배씩 변경)
- L1, L2 규제 중 어떤 규제를 사용할 지 정해야 함
- 중요한 특성이 많지 않으면 L1규제
- 장점
- 학습 속도 빠르고, 예측 빠름
- 매우 큰 데이터, 희소한 데이터에서도 잘 작동
- 수십만~수백만 개의 샘플에 대해서는 slover=’sag옵션 사용 (로지스틱, 릿지) (혹은 SGDClassifier, SDGRegressor 사용)
- 이해가 쉬움
- 단점
- 계수의 값(w)이 왜 이렇게 선정됐는지 명확하지 않은 경우 있음
나이브 베이즈 분류기
- 선형 분류기보다 훈련 속도가 빠름
- 일반화 성능이 조금 떨어짐
- 각 특성을 개별 취급하여 파라미터 학습, 각 특성에서 클래스별 통계를 단순 취합
- GaussianNB: 연속적인 어떤 데이터에도 적용 가능
- 각 클래스 별 피처의 표준편차와 평균을 저장
- BernoulliNB: 이진 데이터
-
각 클래스의 특성 중 0이 아닌 것이 몇 개인지 셈

-
- MultinomialNB: 카운트 데이터, 이산적 데이터에 적용 가능
- BernoulliNB와 MultinomialNB는 대부분 텍스트 데이터 분류 시 사용
- 각 클래스 별 특성의 평균 계산
- 매개변수와 장단점
- MultinomialNB와 BernoulliNB: alpha 매개변수
- 알고리즘이 모든 특성에 양의 값을 가진 가상의 데이터 포인트를 alpha 개수만큼 추가
- alpha가 크면 더 완만, 복잡도 낮아짐
- alpha에 따른 성능 변동은 크지는 않음. but 어느정도 정확도 높일 수 있음
- GaussianNB는 대부분 고차원 데이터셋에 사용, 다른 두 모델은 희소한 데이터 카운트 사용(텍스트)
- MultinomialNB는 보통 0이 아닌 특성이 비교적 많은 데이터셋에서 베르누이보다 성능 높음
- 장단점은 선형모델과 비슷
- 선형 모델로는 학습 시간이 너무 오래 걸리는 매우 큰 데이터셋에는 나이브 베이즈 모델 시도해볼 만 함
- MultinomialNB와 BernoulliNB: alpha 매개변수
결정 트리(Decision tree)
- 결정에 다다르기 위해 T/F 질문을 이어나가며 학습
-
가능한 한 적은 질문으로 문제를 해결하는 것이 목표

-
각 박스를 노드라고 함(node)
- 맨 위 노드는 루트 노드(root node)
- 마지막 노드는 리프 노드(leaf node)
- 타깃 값을 하나만 갖는 노드는 순수 노드(pure node)
-
- 결정 트리를 학습한다?
- 정답에 가장 빨리 도달하는 예/아니오 질문 목록을 학습한다.
- 이 질문들을 테스트라고함( train, test 에서 test 아님!)
- 각 테스트는 하나의 특성에 대해서만 이뤄지므로, 나눠지는 영역은 항상 축에 평행
- 데이터 분할은 결정 트리의 리프가 한 개의 타깃값이 될 때까지 반복
- 한 개의 타깃값: 하나의 클래스나 하나의 회귀 분석 결과
- 정리
- 데이터셋을 노드를 통해 테스트 진행
- 테스트를 통해 데이터들이 이진분류됨
- 미국의 각 주들의 모양처럼 구분하여 나눠짐
- 새로운 데이터 포인트에 대한 예측은 분할된 영역 중 어디에 놓이는지 확인
- 회귀문제에서도 적용 가능
- 각 노드의 테스트 결과에 따라 트리를 탐색, 찾은 노드의 훈련 데이터 평균값이 이 데이터 포인트의 출력이 됨
결정 트리 복잡도 제어
- 모든 리프 노드가 순수 노드가 되면 과대적합됨
- 크게 두 가지 방법으로 제어
- 사전 가지치기(pre-pruning)
- 트리 생성을 일찍 중단
- 트리의 최대 깊이 혹은 리프의 수 제한, 노드가 분할하기 위한 포인트 최소 수량 설정
- max_depth=4 등의 코드로 제한
- 사후 가지치기(=가지치기, post-pruning, pruning)
- 트리를 만든 후 데이터 포인트가 적은 노드를 삭제, 병합
- 사전 가지치기(pre-pruning)
결정 트리 분석
- 트리 모듈의 export_graphviz 함수로 트리 시각화
- 그래프 저장용 텍스트 파일 포맷인 .dot 파일 만듦
-
근데, graphviz를 쓰면 가지 수가 조금만 많아져도 보기 복잡해지는 단점 있음.

특성 중요도
- 전체 트리를 보는 것은 어려우니, 어떻게 작동하는지 요약
- 특성 중요도?
- feature_importances_
- 트리를 만드는 결정에 각 특성이 얼마나 중요한지 평가하는 속성
- 0과 1 사이 숫자
- 특성 중요도 전체 합은 1
- 특성 중요도의 값은 선형 모델 계수와 달리 항상 양의 값
- 값이 낮다고 해당 피처가 중요하지 않은 것은 아님
- 다른 특성이 동일한 정보를 지니고 있어서일 수도 있음
- 노드에서 중요하다고 판단한 피처의 각 클래스를 어떻게 구분하는 지 알 수는 없음
- ex. 반지름 피처가 특성 중요도 높게 나옴.
- 그러면 반지름이 높은 것이 암의 양성 클래스인지, 악성 클래스인지는 알 수 없다
회귀 결정 트리
- 분류에서와 비슷하게 구현됨
- 외삽(extrapolation)을 할 수 없음
- 모든 트리 모델은 훈련 데이터 범위 밖의 포인트는 예측 불가
- 특히, 시계열 데이터에서는 잘 맞지 않는다. (미래 데이터는 훈련 데이터에 없으니까)
- 매개변수와 장단점
- 사전 가지치기
- max_depth, max_leaf_nodes, min_samples_leaf 중 하나만 지정해도 과대적합 방지 충분
- 장점
- 만들어진 모델 시각화 쉬움
- 비전문가 이해가 쉬움 (작은 트리일 때)
- 데이터 스케일에 구애받지 않음
- 각 특성이 개별적으로 처리되는데, 2)의 장점 덕분에 피처의 정규화, 표준화 등 전처리 필요 없음
- 특성의 스케일이 서로 다르거나, 이진 특성과 연속적인 특성이 결합되어있어도 잘 작동
- 만들어진 모델 시각화 쉬움
- 단점
- 사전 가지치기를 사용해도 과대적합되는 경우가 있음
- 일반화 성능이 좋지 않음
- 때문에, 앙상블 방법을 단일 결정 트리의 대안으로 흔히 사용
- 사전 가지치기를 사용해도 과대적합되는 경우가 있음
- 사전 가지치기
결정 트리의 앙상블
랜덤포레스트(random foreset)
- 결정 트리의 과대적합 문제를 피할 수 있음
- 조금씩 다른 결정 트리들의 묶음
- 서로 다른 방향으로 과대적합된 모델들이 평균으로 모이며 과대적합이 줄어듦
- 각 트리는 성능이 좋아야하며, 서로 다른 트리와는 구별되어야함
- ‘랜덤’하게 트리를 만드는 법
- 샘플을 무작위로 뽑음 (부트스트랩)
- 피처를 무작위로 선택 (각 노드에서 피처의 일부만 사용)
- 랜덤포레스트 구축
- 부트스트랩 샘플 생성
- 알고리즘이 각 노드에서 후보 특성을 무작위로 선택
- 이 후보 중 최선의 테스트를 찾음
- 선택할 특성의 수는 max_features 매개변수로 조정
- 랜덤포레스트 분석
- 샘플과 피처를 랜덤화하여 트리를 만들고 그것을 평균냄
- 단일 트리에 비해 더 많은 피처를 사용
- 특성 중요도가 하나의 트리에서 제공하는 것보다 더 신뢰할 수 있음
- 샘플과 피처를 랜덤화하여 트리를 만들고 그것을 평균냄
- 매개변수와 장단점
- 회귀와 분류에서 정말 많이 사용되는 알고리즘
- 성능이 뛰어나고, 매개변수 튜닝을 많이 아내도 잘 작동
- 데이터 스케일을 맞출 필요도 없음
- 단점
- 텍스트 데이터같이 차원이 높고 희소한 데이터에선 잘 작동하지 않음 (선형이 적합)
- 선형 모델보다 많은 메모리, 느린 속도
- n_jobs
- 멀티코어를 활용하여 계산 속도를 빠르게
- n_jobs = -1로 컴퓨터 내 모든 코어 작동 가능 (default = 1)
- n_estimators, max_features, max_depth(이건 가지치기)
- n_estimaotors는 거거익선, 더 많은 트리가 있으면 과대적합을 줄여줘 더 안정적
- 하지만 많을수록 시간과 메모리 많이 먹음
- 가용한 시간과 메모리만큼 많이 훈련시키는 것이 좋다고 한다
- max_features는 트리가 얼마나 무작위가 될지 결정
- 1개의 피처를 선택하면 무작위 선택 > 피처 적용
- max개의 피처를 선택하면 무작위가 아님
- 일반적으로 기본값을 쓰는 것이 좋은 방법 1) 분류 default: max_features = sqrt(n_features) 2) 회귀 default: max_features = n_features
- 회귀와 분류에서 정말 많이 사용되는 알고리즘
그라디언트 부스팅 회귀 트리
- 이름은 회귀이지만, 회귀와 분류에 모두 사용 가능
- 랜덤포레스트와 다른 점
- 이전 트리의 오차를 보완하는 방식으로 순차적으로 트리 생성
- 무작위성이 없음
- 강력한 사전 가지치기 사용
- 보통 하나에서 다섯 정도의 깊지 않은 트리 사용
- 시관과 메모리 적게 듦
- 얕은 트리 같은 간단한 모델을 많이 연결
- 약한 학습기 라고도 함 (weak learner)
- 각 트리는 데이터의 일부에 대해서만 예측을 잘할 수 있기 때문에 트리가 많이 추가될수록 성능 올라감
- 랜덤포레스트보다 매개변수에 민감하지만, 잘 조정하면 더 높은 정확도 제공
- 언제?
- 보통은 더 안정적인 랜덤포레스트를 먼저 적용
- 예측 시간이 중요하거나, 모델에서 마지막 성능까지 쥐어짜야 할 때 그래디언트 부스팅 사용
- 대규모 문제에 그래디언트 부스팅을 적용하려면 xgboost패키지와 파이썬 인터페이스 검토
- 빠르고 튜닝 쉬움
- 매개변수와 장단점
- learning_rate (학습률)
- 이전 트리의 오차를 얼마나 강하게 보정할 지 정하는 매개변수
- 학습률이 크면 보정이 강해짐, 모델 복잡도 상승
- learning_rate를 낮추면 비슷한 복잡도 모델 생성을 위해 n_estimators 올려야 함
- n_estimators (트리의 개수)
- 앙상블에 트리가 더 많이 추가
- 모델 복잡도가 커지며 훈련 세트에서의 실수를 바로잡을 기회 상승
- 크게 하면 모델이 복잡해지고, 과대적합 가능성 올라감
일반적으로 가용한 시간, 메모리 내에서 n_estimators를 맞추고, 적절한 학습률 적용
- max_depth (또는 max_leaf_nodes)
- 일반적으로 작게 설정, 5보다 깊어지지 않게.
- 장점
- 다른 트리 기반 모델과 같이 스케일 조정 필요 없음
- 연속적인 특성에서도 잘 동작
- 희소한 고차원 데이터에서는 잘 작동하지 않음 (텍스트 데이터 등)
- 단점
- 매개변수의 민감성 높음, 그래서 잘 조정해야함
- 훈련 시간이 길다
- learning_rate (학습률)
커널 서포트 벡터 머신(SVM, kernelized support vector machines)
- 인풋에서 단순한 초평면으로 정의되지 않는 더 복잡한 모델을 만들 수 있도록 확장한 것
- 회귀, 분류에 모두 사용가능. 책에서는 분류만 다룸
- 선형 모델과 비선형 특성
- 직선, 초평면은 유연하지 못하여, 저차원 데이터셋에서는 매우 제한적임
- 특성끼리 곱하거나 거듭제곱하는 식으로 새로운 특성을 추가하여 유연하게 만들 수 있음
- 커널 기법(kernel trick)
- 차원 확장
- 어떤 특성을 추가하거나 계산해야할 지 모르거나 연산 비용이 커짐
- 이를 해결하기 위한 커널 기법
- 새로운 특성을 많이 만들지 않더라도 고차원에서 분류기를 학습시킬 수 있음
- 실제로 데이터를 확장하지 않고, 확장된 특성에 대한 데이터들의 거리(스칼라곱)를 계산
- 다항식 커널
- 원래 특성의 가능한 조합을 지정된 차수까지 모두 계산 2. 가우시안 커널(Gaussian) (= RBF 커널(radial basis function))
- 모든 차수의 모든 다항식을 고려
- 특성의 중요도는 고차항이 될수록 줄어듦
- 차원이 무한한 특성 공간에 매핑
- SVM 이해하기
- 학습이 진행되는 동안 SVM은 각 데이터가 결정 경계 구분에 얼마나 중요한 지 배움
- 일반적으로 훈련 데이터의 일부만 결정 경계 생성에 영향을 줌
- 일부: 두 클래스 사이의 경계에 위치한 데이터
- 이런 데이터들을 서포트 벡터 라고 함.
- 새로운 데이터 포인트 예측을 위해서는 서포트 벡터와의 거리를 측정
- 학습이 진행되는 동안 SVM은 각 데이터가 결정 경계 구분에 얼마나 중요한 지 배움
- SVM 매개변수 튜닝
- gamma
- 가우시안 커널 폭의 역수
- 하나의 훈련 샘플이 미치는 영향의 범위
- 작은 값: 넓은 영역
- 큰 값: 제한적
- C
- 선형 모델의 매개변수와 비슷
-
각 포인트의 중요도를 제한 (dual_coef_ 값 제한)
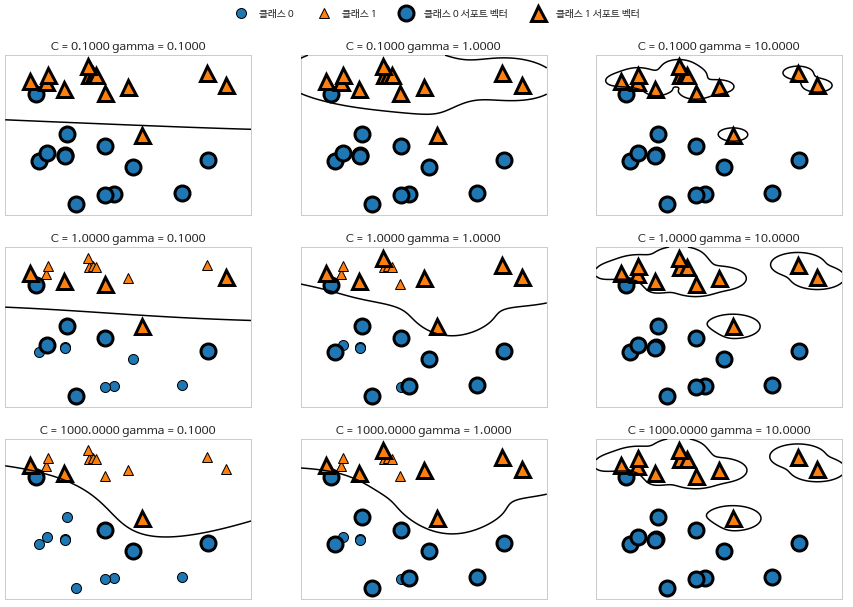
- 그런데!
- SVM은 데이터 스케일에도 매우 민감함
- 특히 입력 특성의 범위가 비슷해야 함.
-
로그스케일로 나타낸 유방암 데이터의 boxplot
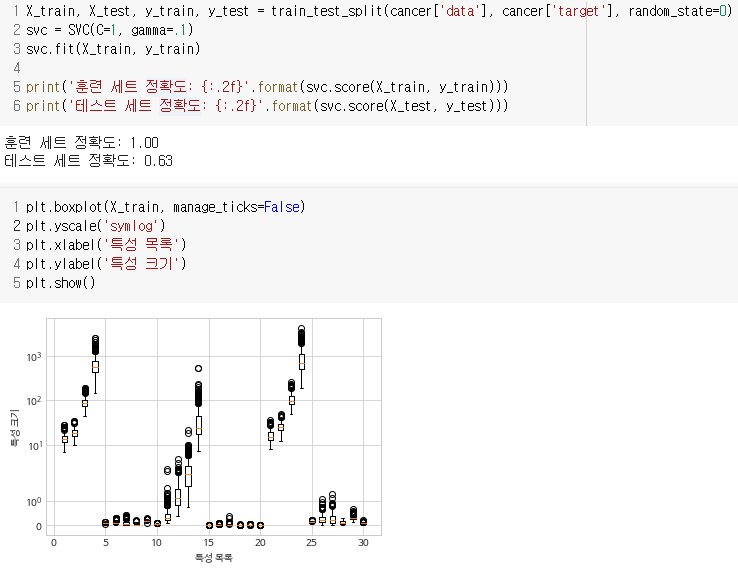
- gamma
- SVM을 위한 데이터 전처리
- 위 문제를 해결하기 위해 모든 특성값을 0과 1 사이로 맞추는 방법 많이 사용
- MinMaxScaler 전처리 메서드 사용할 수 있음
- 매개변수와 장단점
- 장점
- 다양한 데이터셋에서 잘 작동
- 피처가 몇 개 안되더라도 복잡한 결정 경계를 만들 수 있음
- 단점
- 고차원, 저차원에 모두 잘 작동하지만, 샘플이 많을 때는 잘 맞지 않음
- 전처리와 매개변수 설정에 신경을 많이 써야함 (요즘 랜덤포레스트나 그래디언트 부스팅 같은 트리 모델을 많이 쓰는 이유)
- 분석도 어려우며, 이해도 어렵고 비전문가에게 설명하기도 난해함
- 특성이 비슷한 단위이고, 스케일이 비슷하면 시도해볼만 함
- ex. 모든 값이 픽셀의 컬러 강도
- 매개변수 C
- 각 포인트들의 중요도 제한
- 어떤 커널을 사용할 지
- 실습한 것은 RBF커널
- 그 외에도 커널 많음!
- 그 커널에 따른 매개변수
- RBF는 gamma였음
- 장점
신경망(딥러닝)
책에서 다루는 것은 다층 퍼셉트론 (MLP, multilayer perceptrons)
피드포워드(feed-forward)신경망, 또는 신경망 이라고도 함

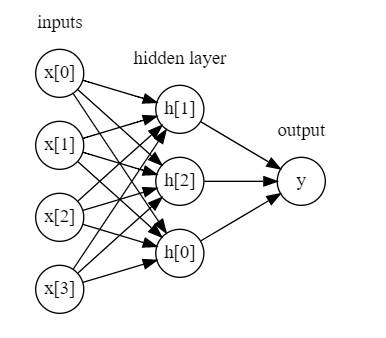
- 선형모델과 MLP 시각화 차이
- MLP에서는 가중치 합을 만드는 과정이 여러 번 반복됨 (선형 모델에서는 가중치의 합 [ y^ = wx + b ]에서 끝난다)
- 중간 단계를 구성하는 은닉 유닛(hidden unit)을 계산
- 이를 이용하여 가중치 합을 계산, 최종 결과 산출
- 이런 모델은 많은 계수(또는 가중치)를 학습해야함
- 입력과 은닉층 사이의 계수
- 은닉층의 은닉 유닛 사이의 계수
- 은닉 유닛과 출력 사이의 계수
- 여러 가중치의 합을 계산하는 것은 수학적으로는 하나의 가중치 합을 계산하는 것과 같음
- 모델을 선형보다 더 복잡하게 만들기 위해 비선형 함수를 적용함
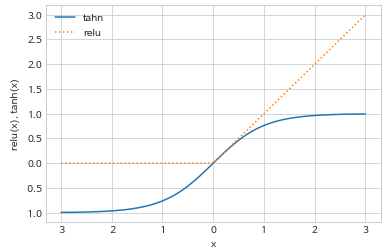
- 렐루 (ReLU, rectified linear unit)
- 0 이하의 값은 잘라버림 - 하이퍼볼릭 탄젠트(tanh, hyperbolic tangent)
-
작은 입력값은 -1로 수렴, 큰 입력값은 1로 수렴
- h[0] = tanh(w[0,0] * x[0] + w[1,0] * x[1] + w[2,0] * x[2] + w[3,0] * x[3] + b[0])
- h[1] = tanh(w[0,1] * x[0] + w[1,1] * x[1] + w[2,1] * x[2] + w[3,1] * x[3] + b[1])
- h[2] = tanh(w[0,2] * x[0] + w[1,2] * x[1] + w[2,2] * x[2] + w[3,2] * x[3] + b[2])
- y^ = v[0] * h[0] + v[1] * h[1] + v[2] * h[2] + b
- w는 입력 x와 은닉층 h 사이의 가중치
- v는 은닉층 h와 출력 y^ 사이의 가중치
- x는 입력 특성, y^는 계산된 출력, h는 중간 계산값
- 정해야할 매개변수는 은닉층의 유닛 수
- 작을 경우 10개 정도로 충분하지만, 복잡한 데이터셋에선 10,000개가 될 수도 있음
-
은닉층을 추가할 수도 있음
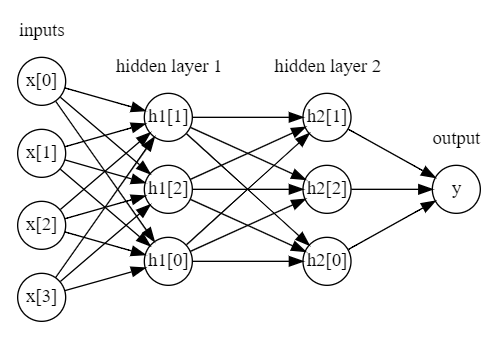
- 이렇게 많은 은닉층으로 구성된 대규모 신경망이 생기며 이를 딥러닝이라고 부르게됨..
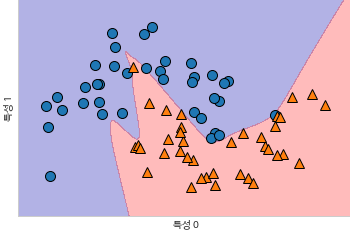
- 신경망 튜닝
-
유닛수 10개

-
유닛수 100개

-
유닛수 10개 * 은닉층 2개
-
유닛수 10개 * 은닉층 2개 + tanh 활성화 함수
-
alpha로 L2 규제, 가중치를 0에 가깝게 감소, 모델의 복잡도 제어
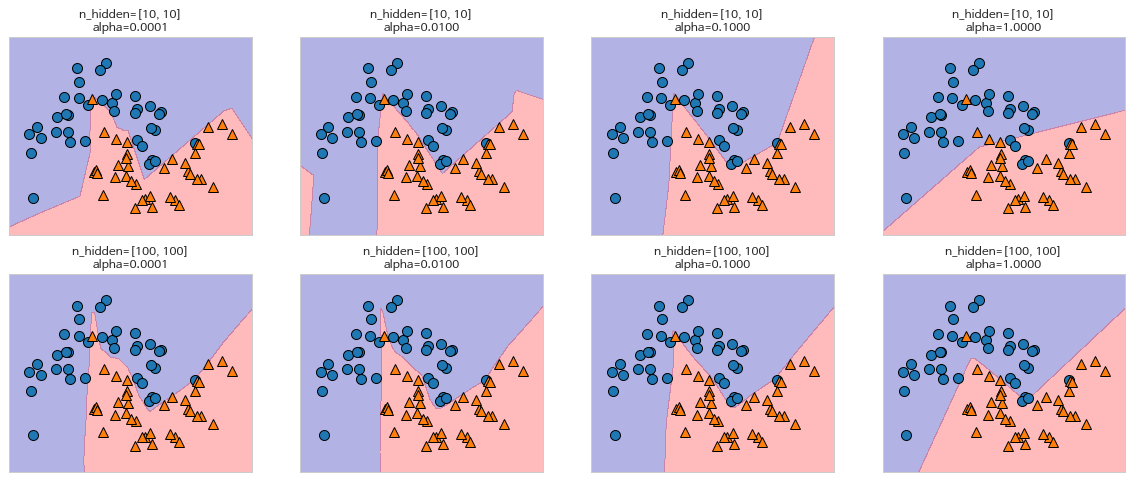
-
매개변수가 동일하더라도, 무작위한 초기값에 따라 모델이 달라짐 (random_state)

-
MLP모델도 데이터 스케일 표준화 필요 스케일 조정 시 convergence경고 출력 시 반복 횟수 늘려줘야함
-
- MLPClassifier와 MLPRegressor는 손쉬운 인터페이스를 제공하지만, 일부만 만들 수 있음
- 더 복잡한 모델을 위해서는 scikit-learn보다 keras, lasagna, tensorflow, PyTorch 등 1) lasagna: theano 라이브러리에 구축한 것 2) keras: tensorflow, theano 중 선택 가능 3) PyTorch: 페이스북에서 오픈 소스로 공개된 라이브러리
- 매개변수와 장단점
- 장점
- 대량의 데이터에 내재된 정보를 잡아냄
- 매우 복잡한 모델을 만들 수 있음
- 충분한 연산 시간, 데이터로 매개변수를 잘 조정하면 다른 알고리즘보다 뛰어난 성능
- 단점
- 학습이 오래 걸림
- 전처리에 유의 (SVM과 같이, 모든 피처가 같은 의미를 가진 동질의 데이터에서 잘 작동)
- 장점
- 신경망의 복잡도 추정
- 매개변수는 은닉층 개수와 은닉층 유닛 수
- 1~2개에서 시작하여 보통 피처 수와 비슷하게 설정.
- 보통 수천 초중반을 넘지는 않음
- 학습된 가중치, 계수의 수가 복잡도를 이해하는데 도움을 줌
- 피처 100개, 은닉 유닛 100개 1) 피처 - 은닉층: 100 * 100 = 10,000개의 가중치 2) 은닉층 - 출력층: 100 * 1 = 100개의 가중치
- 총 학습해야 할 가중치 수: 10,100
- 피처 100개, 은닉 유닛 100개 * 2개의 은닉층 1) 피처 - 은닉층a: 100 * 100 = 10,000 2) 은닉층a - 은닉층b: 100 * 100 = 10,000 3) 은닉층b - 출력층: 100 * 1 = 100
- 총 가중치 수: 20,100
- 피처 1,000개, 은닉 유닛 1,000개 1) 피처 - 은닉층: 1,000 * 1,000 = 1,000,000 2) 은닉층 - 출력층: 1,000 * 1 = 1,000
- 총 가중치 수: 1,001,000
- 피처 1,000개, 은닉 유닛 1,000개 * 2개의 은닉층 1) 피처 - 은닉층a: 1,000 * 1,000 = 1,000,000 2) 은닉층a - 은닉층b: 1,000 * 1,000 = 1,000,000 3) 은닉층b - 출력층: 1,000 * 1 = 1,000
- 총 가중치 수: 2,001,000
- 일반적으로 매개변수 조정하는 법
- 일반적으로 충분히 과대적합되어 문제를 해결할 수 있는 큰 모델 생성
- 신경망 구조를 줄이거나,
- alpha값 증가시켜 규제 강화
- solver매개변수
- adam (default)
- 대부분 잘 작동
- 데이터 스케일에 민감
- 그래서 z표준화 해주는 것이 중요
- lbfgs
- 안정적
- 규모가 크거나 대량의 데이터셋에선 시간이 오래걸림
- sgd
- 여러 매개변수와 함께 튜닝하여 좋은 성능 발휘 가능
- 매개변수는 은닉층 개수와 은닉층 유닛 수
- 분류 예측의 불확실성 추정
- 분류 예측의 결과에 얼마나 확신하는지?
- 1종, 2종 오류
- scikit-learn 분류기에서는 decision_function과 predict_proba
- 대부분의 분류 모델은 적어도 둘 중 하나는 지원 1. decision_function (결정 함수)
- 이진 분류에서 decision_function의 반환값은 (n_samples, )
- 각 샘플이 하나의 실수 값 반환
- 값? 데이터 포인트가 클래스 1에 속한다고 믿는 정도
- 양수 값은 양성 클래스(1) 의미, 음수 값은 음성 클래스(0) 의미
- classes_ 속성의 순서에 따라 양성[1], 음성 클래스[0] 구분 가능 2. predict_proba (예측 확률)
- 각 클래스에 대한 확률
- decision_function의 출력보다 이해하기 더 쉬움
- (n_samples, 2)
- 첫 원소: 첫 번째 클래스일 확률
- 두 번째 원소: 두 번째 클래스일 확률
두 원소 합은 1
- 불확실성이 얼마나 잘 반영되었는지는 매개변수와 모델에 달림
- 과대적합 모델은 예측 결과가 잘못되었어도 예측의 확신이 강함
- 반면, 복잡도가 낮은 모델은 예측에 불확실성이 더 많음
- 보정(calibration) - 모델의 불확실성 = 정확도 일 때 보정되었다 라고 함. 3. 다중 분류에서 불확실성
- (n_samples, n_classes)
- 각 데이터 포인트마다 점수들 중 가장 큰 값을 찾아 예측 결과 재현 가능
- 버그를 방지하기 위해서는 classes_[n] 사용하자!
- 분류 예측의 결과에 얼마나 확신하는지?
댓글남기기