비지도 학습, 데이터 전처리 스터디 내용 요약

업데이트: March 15, 2020

3. 비지도학습과 데이터 전처리

비지도 학습

unsupervised learning

비지도 학습의 종류

비지도 변환(unsupervised transformation)
- 데이터를 새롭게 표현하여 사람이나 다른 머신러닝 알고리즘이 쉽게 해석할 수 있도록 만드는 알고리즘
- 대표적으로는, 차원 축소(dimensionality reduction)
  - 고차원 데이터의 피처 수를 줄이고, 꼭 필요한 데이터만 남기는 방법
  - 대표적인 차원 축소로 시각화를 위해 데이터셋을 2차원으로 변경하는것
- 데이터 구성 단위나 성분을 찾기도 함
  - ex. 텍스트 문서에서 주제를 추출하는 일
군집 알고리즘
- 데이터를 비슷한 것끼리 그룹으로 묶는 것
  - ex. sns 사진 분류
  - 찍은 사람 뿐만 아니라, 사진의 얼굴이 누구인지 군집화

비지도 학습의 도전 과제

비지도 학습에서 어려운 점들
- 유용한 것을 학습했는가?
- 이게 올바른 출력인가?
- 그러니까, 모델이 일을 잘 하고있는가?
- ex. 군집 알고리즘이 옆모습, 앞모습을 분류하였음 → 원하는 방향은 아님.
- 그런데 위와 같은 상황에서 우리가 원하는 분류의 기준을 알려줄 수가 없음
- 학습 결과를 평가하기 위해 직접 확인하는 것이 유일한 방법인 경우가 많음
비지도 학습 알고리즘은 EDA단계에서 많이 사용
지도 학습의 전처리 단계에서도 사용
- 비지도 학습의 결과로 새롭게 표현된 데이터를 사용하여 학습하면
  - 정확도가 좋아지는 경우도 있고
  - 시간과 메모리 절약 가능

데이터 전처리와 스케일 조정

간단한 예시 살펴보기
```
  mglearn.plots.plot_scaling()
```
여러 가지 전처리 방법

StandardScaler
- Z표준화, 평균0, 분산1
  - (x - 평균) / 표준편차
- 피처의 최솟값과 최댓값 크기 제한하지 않음
RobustScaler
- 특성들이 같은 스케일 갖게됨
- StandardScaler과 달리, 중간 값(median)과 사분위 값(quartile)을 사용
  - (x - q₂(median)) / (q₃ - q₁) (데이터에서 중간값 빼고 q₃ - q₁범위로 나눔)
- 이상치(outlier)에 영향을 받지 않고 로버스트함
MinMaxScaler
- 모든 데이터가 0과 1 사이에 위치하도록 데이터 변경
  - x - x_min / x_max - x_min (데이터에서 최솟값을 빼고 전체 범위로 나눔)
Normalizer
- 피처 벡터의 유클리디안 길이가 1이 되도록 데이터 포인트 조정
- 지름이 1인 원에 데이터들을 투영
  - 데이터가 다른 비율로 스케일이 조정됨
- 이런 정규화(Normalization)는 피처 벡터의 길이는 상관 없고 방향(각도)이 중요할 때 사용

데이터 변환하기
- 항상 훈련 세트와 테스트 세트에 같은 변환을 적용해야함
  - 테스트 세트에 transform 메서드 적용될 때, 테스트 세트의 최소, 최댓값이 아닌 훈련 세트의 그것들에 적용됨
  - x_test - x_train_min / x_train_max - x_train_min ```python import sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler() # StandardSclaer(), RobustScaler(), Normalizer()

# y_train은 넣지 않음 # 스케일링한 결과를 원하지는 않으니까! scaler.fit(X_train)

# 실제 데이터 변환은 transform 메서드로 X_train_scaled = scaler.transform(X_train) X_test_scaled = scaler.transform(X_test)

# 더 효율적인 방법을 사용해보자 scaler = MinMaxScaler() X_train_scaled = scaler.fit(X_train).transform(X_train) # 방법 1 X_train_scaled = scaler.fit_transform(X_train) # 방법 2, 더 효율적 X_test_scaled = scaler.transform(X_test) ```

차원 축소, 특성 추출, 매니폴드 학습
비지도학습을 사용하는 가장 일반적인 이유
1. 시각화
2. 데이터 압축
3. 추가 처리 (주로 지도 학습에 사용하기 위해서)

주로 학습할 것

주성분 분석(PCA, principal component analysis)
- 위와 같은 용도로 가장 간단하고 흔히 사용하는 알고리즘
비음수 행렬 분해(NMF, non-negative matrix factorizaion)
- 특성 추출에 널리 사용
t-SNE(t-distributed stochastic neighbor embedding)
- 2차원 산점도를 이용해 시각화 용도로 많이 사용

주성분 분석(PCA)

피처들이 통계적으로 상관관계가 없도록 데이터셋을 회전시키는 기술
- 회전 뒤 데이터를 설명에 있어 중요도에 따라 종종 새로운 특성 중 일부만 선택
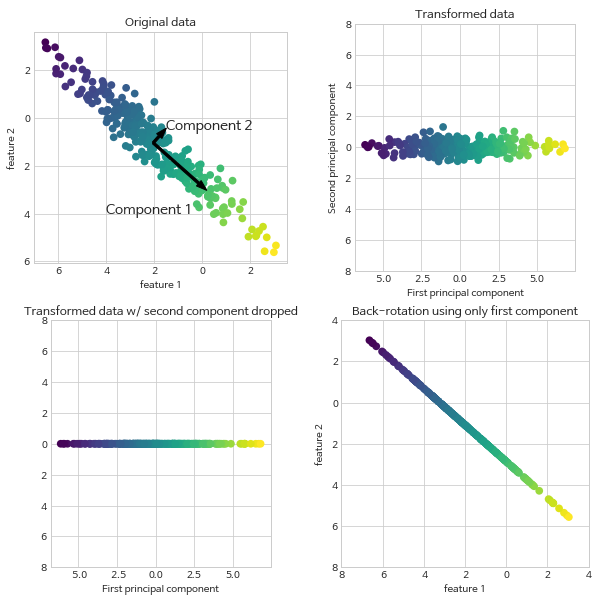
1. 분산이 가장 큰 방향을 찾음 (그림(1,1)에서 Component1 방향)
  - 상관관계가 큰 방향
2. 찾은 방향에서 직각이 되는 방향 중 가장 정보를 많이 포함한 방향 찾음
  - 고차원에선 수많은 직각 방향이 존재
  - 주성분(principal component)
    - 주된 분산의 방향을 주성분이라고 함
    - 그림에서 화살표의 방향은 사실 의미 없음. (Com1이 왼쪽 위든, 오른쪽 아래든)
    - 일반적으로 원본의 피처의 개수만큼의 주성분 존재
3. 데이터에서 평균을 빼고 회전(그림(1,2)), 중심을 원점에 맞춤
  - 두 축은 연관되어있지 않음
  - 변환된 데이터의 상관관계 행렬(correlation matrix)이 대각선 방향을 제외하고는 0이 됨
    - 상관관계 행렬: 공분산 행렬을 정규화한 것
4. 주 성분의 일부만 남겨 차원 축소 용도로 사용 가능 (그림(2,1))
  - 단순히 일부만 남기는 것이 아님
  - 가장 유용한 방향을 찾아, 그 방향의 성분을 유지 (그림에선 첫 번째 성분 유지)
5. 데이터에 평균을 더한 후 다시 회전(그림(2,2))
  - 이 데이터들은 원래 특성 공간에 놓여있지만, 축소된 차원의 성분만 가지고 있음
  - 이 과정에서 노이즈를 제거하거나 주성분에서 유지되는 정보 시각화하는데 종종 쓰임
가장 널리 사용되는 분야는 고차원 데이터셋 시각화
PCA를 이용한 데이터 시각화
- 해석하기가 쉽지는 않다는 단점
- PCA를 이용한 시각화는 노트북 참조

        from sklearn.decomposition import PCA
        # 처음 두 개의 주성분만 유지
        pca = PCA(n_components=2)

        # PCA모델 생성
        pca.fit(X_scaled)

        # 처음 두 개의 주성분을 사용해 데이터 변환
        X_pca = pca.transform(X_scaled)

        # 이후 산점도로 나타내보기

PCA객체가 학습(fit)될 때 components_속성에 주성분 저장됨
주성분 시각화
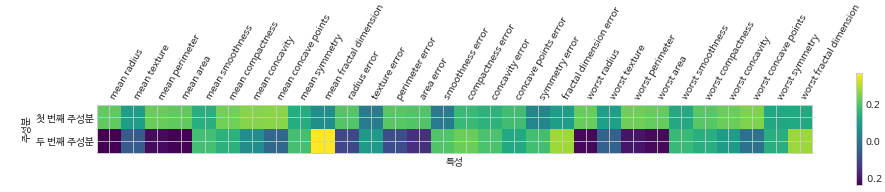
- 첫 번째 주성분은 모두 부호가 같음 (화살표 방향, 즉, 양수냐 음수냐는 의미가 없음)
  - 모든 특성 사이에 공통의 송호관계가 있다는 뜻
- 두 번째 주성분은 부호가 섞여있고, 두 주성분 모두 30개의 특성이 있음
  - 모든 특성이 섞여있기 때문에, 축이 가지는 의미를 설명하기 쉽지 않다
고유얼굴(eignenface) 특성 추출
- 얼굴인식
  - 새로운 얼굴 이미지가 DB에 있는지 찾는 작업
  - 해결 방법1
  - 각 사람을 다른 클래스로 분류하는 분류기 생성
  - 이 경우, 보통 사람 수는 많지만, 1인 당 사진 수는 적음 - 훈련 데이터가 적다
  - 그럼, 대규모 모델을 다시 훈련시키지 않고 새로운 얼굴을 쉽게 추가하는 방법 없을까?
- 1-최근법 이웃 분류기
```
      from sklearn.neighbors import KNeighborsClassifier
      # 데이터를 훈련 세트와 테스트 세트로 나눔
      X_train, X_test, y_train, y_test = train_test_split(
          X_people, y_people, stratify=y_people, random_state=0)
      # 이웃 개수를 한 개로 하여 KNeighborsClassifier 모델을 만들기
      knn = KNeighborsClassifier(n_neighbors=1)
      knn.fit(X_train, y_train)
      print("1-최근접 이웃의 테스트 세트 점수: {:.2f}".format(knn.score(X_test, y_test)))
      # 0.23
```
  - 원본 픽셀 공간에서 거리를 계산하는 것은 효과적이지 않음
  - 새로운 이미지에서 얼굴이 조금만 오른쪽으로 가도 다른 사진으로 분류하기 때문
  - 주성분으로 변환하여 거리를 계산하면 정확도가 높아지지 않을까?
- PCA의 화이트닝 옵션
  - 주성분의 스케일이 같아지도록 조정 (변환한 후 StandardScaler를 적용하는 것과 같음)
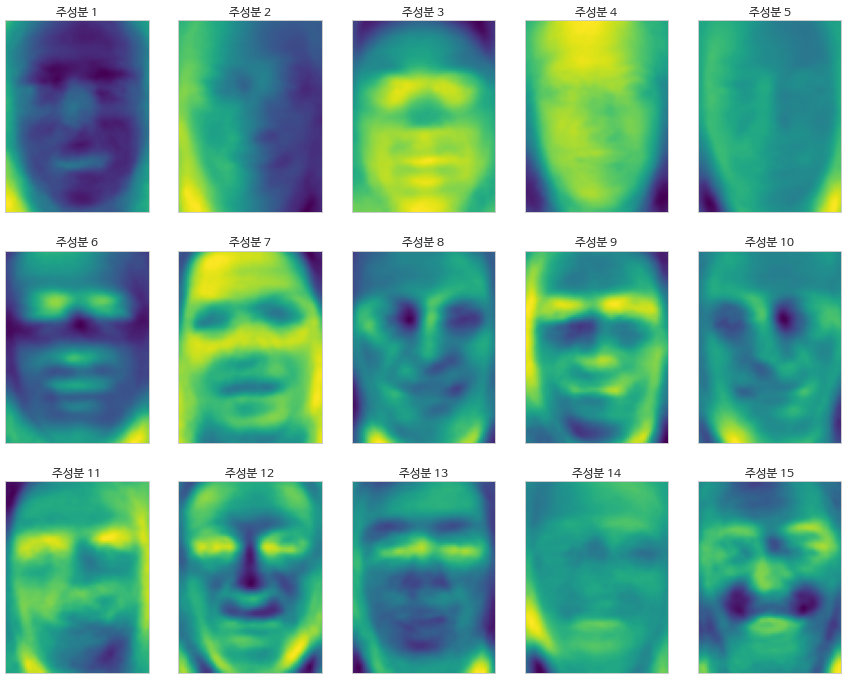
  - 사람이 이해하는것과 알고리즘이 데이터를 해석하는 방식은 상당히 다르다.
  - 특히 이미지와 같은 경우엔 더더욱!
  - 주성분을 이해하기 위해, 몇 개의 주성분을 사용해 원본 데이터를 재구성해보기(무서어)

비음수 행렬 분해(NMF, non-negative matrix factorization

유용한 특성을 뽑아내기 위한 알고리즘
PCA와 비슷, 차원 축소에 사용할 수 있음
섞여있는 데이터에서 원본 성분을 구분 가능
- 예를들어 여러 사람의 목소리 오디오 데이터 → 목소리 구분
- 여러 악기로 이뤄진 음악
NMF에서는 음수가 아닌 성분과 계수 값을 찾음
- 주성분과 계수가 모두 0보다 크거나 같아야함
- 음수가 아닌 피처를 가진 데이터에만 적용 가능!
- 데이터가 (0,0)에서 가는 방향!
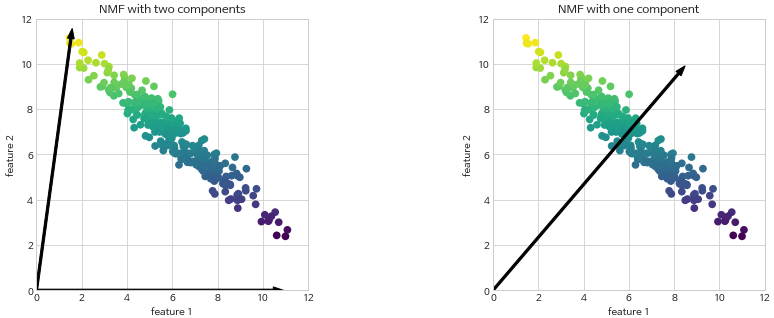
- 하나의 성분을 사용한다면, 데이터를 가장 잘 표현하는 성분으로 향함
- 성분 수를 줄이면 특정 방향이 제거되는 것 뿐만 아니라 전체 성분이 바뀜!
  - PCA는 성분이 바뀌지는 않음
- NMF는 성분이 특정 방식으로 정렬도 되어있지 않아, 순서도 없음 (파이썬 set처럼)

t-SNE를 이용한 매니폴드 학습

매니폴드 학습 (manifold learning) 시각화 알고리즘들은 복잡한 매핑을 만들어 PCA보다 더 나은 시각화 제공
- 그 중에서도 t-SNE (t-Distributed Stochastic Neighbor Embedding)을 많이 사용
- 목적이 시각화라, 3개 이상의 피처를 뽑는 경우가 거의 없음
- 변환 적용한 훈련 데이터에만 적용 가능, 테스트 세트에는 적용 불가.
  - 새로운 세트에 적용 불가
- EDA에는 유용하나, 지도학습용으로는 사용 X

군집(clustering)

데이터셋을 클러스터(cluster)라는 그룹으로 나누는 작업
그룹내 유사, 그룹간 이질적
분류 알고리즙과 비슷하게, 각 데이터 포인트가 어느 클러스터에 속하는지 할당(예측)

k-평균 군집(k-means clustering)

데이터의 어떤 영역을 대표하는 영역 찾음
데이터 포인트를 가장 가까운 클러스터 중심에 할당
클러스터에 할당된 데이터들의 평균으로 중심 재설정

2~3 반복 후 클러스터에 할당되는 데이터 포인트에 변화 없을 시 종료

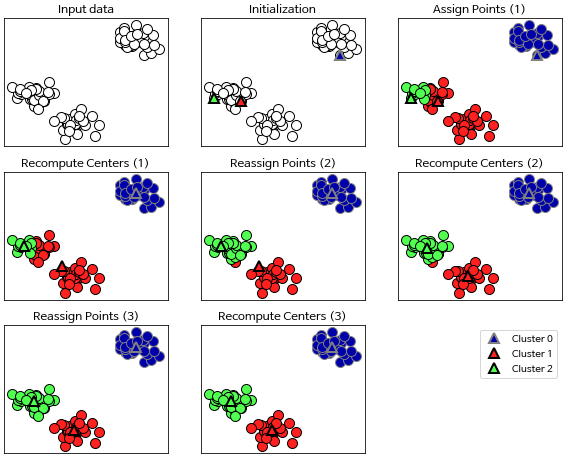
새로운 데이터 포인트가 주어지면, 가장 가까운 클러스터 중심을 할당

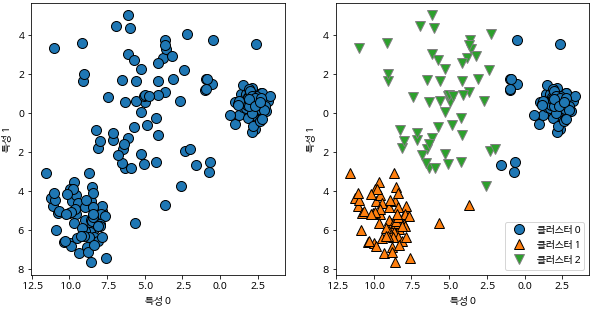
 from sklearn.cluster import KMeans
 kmeans = KMeans(n_cluster=3)
 # 모델 생성
 kmeans.fit(X)
 # 레이블 확인: labels_ 속성
 print('레이블 확인: {}'.format(kmeans.labels_)) # [0, 0, 1, 2, 0, 2, 1, 1, 2 ...]
 # 클러스터 센터 확인
 kmeans.cluster_centers_

레이블 자체에는 큰 의미가 없고, 의미를 알기 위해선 직접 데이터 확인해봐야함
- 같은 데이터로 다시 훈련시켰을 때, 분류 결과는 같지만 레이블 이름은 바뀔수도 있음
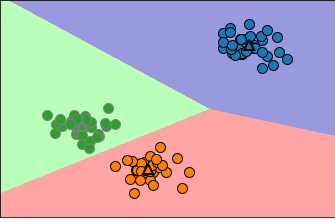
k-평균 알고리즘이 실패하는 경우
- 데이터셋의 클러스터 수를 알고있더라도 항상 구분할 수 있는 것은 아님
- 클러스터 중심이 하나뿐이므로, 클러스터는 둥근 형태 나타냄
  - 그래서 이 알고리즘은 비교적 간단한 형태를 구분 가능
- 또한, k-평균은 모든 클러스터 반경이 똑같다고 가정
- 그 중심 사이의 정확히 중간에 경계 그림
  - 클러스터 0, 1을 보면 중심에서 조금 떨어진 데이터도 포함함
  - 원형이 아닌 데이터셋에선 잘못 구분할 수 있음
    - 모든 방향을 중요시함
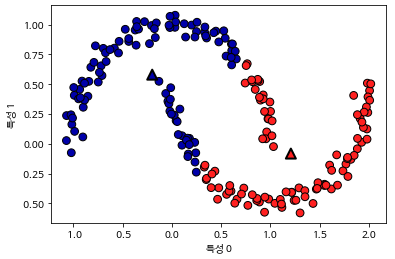
  - 복잡한 모양에서도 구분을 잘 하지 못함
벡터 양자화(vector quantization)
- PCA: 분산이 큰 방향 찾기
- NMF: 데이터의 극단 또는 일부분에 상응되는 중첩할 수 있는 성분 찾기
- k-means: 클러스터 중심, 즉 데이터들을 하나의 성분으로 표현
  - 이렇게 데이터들을 하나의 성분(중심)으로 분해하는 관점으로 보는 것을 벡터 양자화
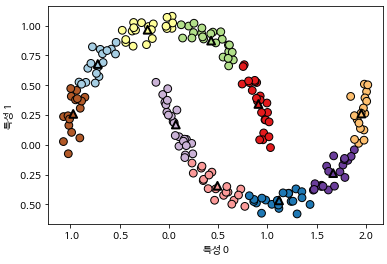
  - k-means는 차원보다 높은 클러스터 지정 가능
  - transform(X)하여, 데이터와 클러스터 중심간의 거리 표현 가능
    distance_features = kmeans.transform(X) print("클러스터 거리 데이터의 형태:", distance_features.shape) print("클러스터 거리:\n", distance_features)
단점
- k-means의 난수 초깃값에 따라 출력이 달라짐
- 클러스터의 모양을 가정하고있어, 활용 범위 제한적
- 클러스터의 수를 지정해줘야함.
  - 실무에서는 클러스터 수를 모르는 경우가 많을것임
- 이러한 단점을 개선한 알고리즘은 없을까?

병합 군집(agglomerative clustering)

각 포인트를 하나의 클러스터로 지정
종료 조건을 만족할 때까지 가장 비슷한 두 클러스터를 합침
- sklearn에서 사용하는 종료 조건은 클러스터 수
- linkage(연결) 옵션에서 ‘비슷한’을 어떻게 측정할 지 지정
  1. ward(default) → 분산을 가장 작게 증가시키는 두 클러스터를 합침 → 그래서 크기가 비교적 비슷한 클러스터가 생성됨
  2. average → 포인트 사이의 평균 거리가 가장 짧은 두 클러스터를 합침
  3. complete(최대연결) **→ 포인트 사이의 최대 거리가 가장 짧은 두 클러스터를 합침
    - 각 클러스터에 속한 포인트 수가 많이 다를 때에 2, 3번의 방법이 나을 수 있음

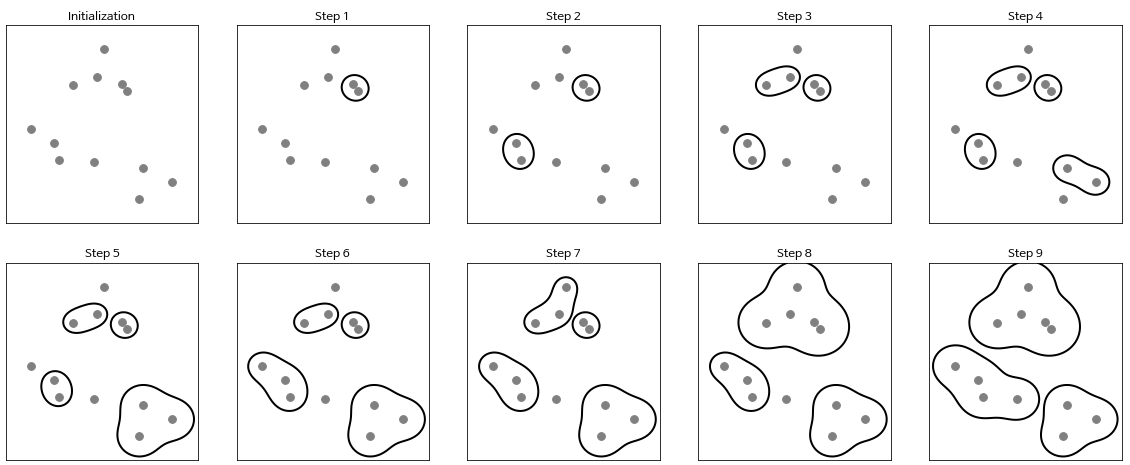
새로운 데이터 포인트에 대해서는 예측을 할 수 없음
- predict 메서드 없음
- 대신 훈련 세트로 모델 생성 후, 클러스터 소속 정보를 얻기 위해 fit_predict 메서드 사용
여전히 클러스터 수를 지정해줘야하는 문제, 해결할 수 없을까?

계층적 군집과 덴드로그램

병합 군집은 계층적 군집을 만듦(hierarchical clustering)
덴드로그램(dendrogram)
- 다차원의 계층 군집을 시각화
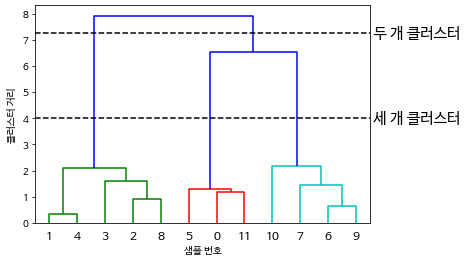
- 가지의 길이: 클러스터 간 거리
- 트리모델과 비슷하게 leaf들과 노드같은 것들로 묶여있음
하지만 여전히 복잡한 데이터셋은 구분하지 못함
복잡한 것들도 구분해줄 수 있는 알고리즘 없나?

DBSCAN(density-based spatial clustering of applications with noise)

장점
- 클러스터 개수를 미리 지정하지 않아도 됨
- 복잡한 세트에서도 구분 가능
- 클래스에 속하지 않는 데이터 포인트 구분 가능
- 병합 군집이나 k-means 보다는 느리지만, 큰 데이터에서도 가능
밀집 지역(dense region)
- DBSCAN에서는 데이터가 밀집된 지역을 찾음
- 데이터의 밀집 지역이 한 클러스터를 구성
- 비교적 비어있는 지역을 경계로 다른 클러스터와 구분
- 핵심 샘플(핵심 포인트)
  - 밀집 지역에 있는 데이터 포인트
매개변수
- min_samples, eps
- 한 데이터 포인트에서 eps 거리 안에 데이터가 min_samples 만큼 들어있으면 그 데이터 포인트를 핵심 샘플로 분류
- eps보다 가까운 핵심 샘플은 DBSCAN에 의해 동일한 클러스터로 합쳐짐
작동 순서
1. 시작할 때 무작위로 포인트 선택
2. eps 거리 안의 모든 포인트 찾음
  - eps 거리 안의 포인트 수가 min_samples보다 적으면 잡음(noise)으로 분류
  - min_samples보다 많으면, 핵심 포인트로 레이블, 새로운 클러스터 레이블 할당
3. 레이블 할당된 데이터들로부터 eps거리 안의 모든 이웃 살핌
  - 어떤 레이블에도 할당이 안되어있으면, 전에 만든 레이블 할당
  - 만약 핵심 샘플이면, 그 포인트의 이웃을 차례로 방문
4. eps 거리 안에 핵심 샘플이 없을때까지 진행
  - DBSCAN에서 포인트 종류
  1. 핵심 포인트
  2. 경계 포인트(핵심 포인트에서 eps 거리 안에 있는 포인트)
  3. 잡음 포인트(noise)
DBSCAN을 한 데이터셋에 여러번 적용하면?
- 핵심 포인트, 잡음 포인트는 동일
- 경계 포인트는 방문 순서에 따라 클러스터 레이블이 다를 수 있음
  - 하지만 중요한 이슈는 아니고, 경계 포인트 수 자체가 많지도 않음

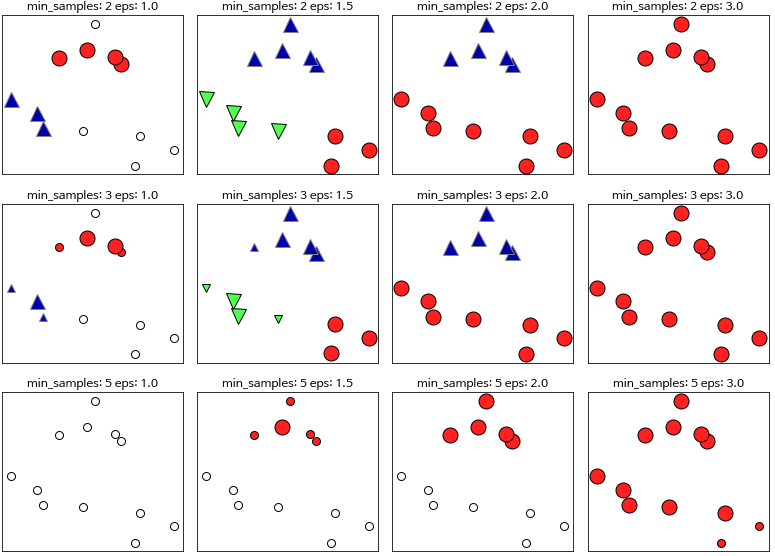
eps
- 가까운 포인트의 범위를 결정
- 너무 크면 하나의 클러스터에 속하고, 너무 작으면 핵심포인트를 만들지 못하거나 모두 잡음
- 적절값을 잘 찾기 위해선 MinMaxScaler나 StandardScaler로 조정
min_samples
- 데이터가 덜 모인 지역의 포인트를 잡음처리할 것인지, 클러스터로 속하게 할 것인지 결정
레이블 할당값을 조심해야한다!
- 클러스터 레이블을 그대로 사용할 경우, 노이즈인 -1값이 어떤 결과를 불러올지 모름

군집 알고리즘 비교 및 평가

군집 알고리즘은 알고리즘이 잘 작동하는지 평가하거나 비교하기가 매우 어렵다.

타깃값으로 군집 평가하기
- 군집 알고리즘의 결과를 실제 정답 클러스터와 비교
- 1(최적)과 0(무작위 분류)사이의 값을 제공하는
  - ARI(adjusted rand index) > 값이 음수가 될 수도 있음
  - NMI(normalized mutual information)
- 가장 많이 하는 실수는
  - adjusted_rand_score나 normalized_mutual_info_score와 같은 군집용 측정 도구를 사용하지 않고, accuracy_score를 적용하는 것
  - 정확도(accuracy_score)는 클러스터의 레이블 이름이 실제 레이블 이름과 맞는지 확인
    - 클러스터 레이블은 이름에 의미가 없기때문에 결과가 다를 수 있음
      from sklearn.metrics import accuracy_score # 포인트가 클러스터로 나뉜 두 가지 경우 clusters1 = [0, 0, 1, 1, 0] clusters2 = [1, 1, 0, 0, 1] # 모든 레이블이 달라졌으므로 정확도는 0 print("정확도: {:.2f}".format(accuracy_score(clusters1, clusters2))) # 같은 포인트가 클러스터에 모였으므로 ARI는 1 print("ARI: {:.2f}".format(adjusted_rand_score(clusters1, clusters2))) # 정확도: 0.00 # ARI: 1.00
실루엣 계수(silhouette coefficient)
- 근데 사실 타깃값이 없는 경우가 더 많음 (알면 바로 분류기 모델을 사용하면 되는디)
- 클러스터의 밀집 정도를 계산하는 것
- 높을수록 좋으며 최대는 1
- 그런데 이 계수도 잘 동작하지는 않으며, 복잡한 경우에는 평가가 잘 맞지 않음
가장 좋은 평가 전략은 견고성 기반 지표 (robustness-based)
- sklearn에는 아직 없음
- 데이터에 노이즈를 추가하거나 여러가지 매개변수 설정으로 알고리즘 실행, 결과 비교
  - 매개변수등을 변화시켜 반복했을 때 결과가 일정하면 신뢰 가능
결국 클러스터가 내가 원하는대로 구분했는지 보려면 직접 확인해야함
- 다른 방법 찾아보기

이상치 검출(outlier detection)
- 특이한 것을 찾아내는 것
- 군집화 중 노이즈에 해당되는 데이터들을 확인해보니 이상한 사진들인 경우 등..
군집 알고리즘 요약
- 종류
  - k-means, DBSCAN, 병합 군집
- k-means, 병합 군집은 클러스터 수 지정 가능
- DBSCAN은 eps와 클러스터 크기 매개변수로 조정 가능
- k-means
  - 클러스터 중심을 사용해 구분
  - 클러스터 중심이 각 클러스터 데이터들을 대표하기 때문에, 분해로도 볼 수 있음
- DBSCAN
  - 클러스터에 할당되지 않는 잡음 포인트 인식 가능
  - 클러스터 수 자동 결정
  - 복잡한 클러스터의 모양 인식 가능(two_moons예시)
  - 크기가 많이 다른 클러스터를 만들어내곤 함(장,단점 공존)
- 병합 군집
  - 전체 데이터의 분할 계층도 생성
  - 덴드로그램으로 시각화 가능

서울숲 미세먼지

비지도 학습, 데이터 전처리 스터디 내용 요약

3. 비지도학습과 데이터 전처리

비지도 학습

비지도 학습의 종류

비지도 학습의 도전 과제

데이터 전처리와 스케일 조정

차원 축소, 특성 추출, 매니폴드 학습

군집(clustering)

댓글남기기

참고

실무를 위한 ABtest Study

글또 5기 후기

그래서 무슨 지표를 보라는걸까

dump를 알기 전까지 한 모든 삽질