모델 평가와 성능 향상 스터디 내용 요약

업데이트: March 27, 2020

5. 모델 평가와 성능 향상

다룰 내용
- R^2값 외에 모델을 평가하는 방법
- 모델의 일반화 성능을 올리기 위한 지도 학습 모델의 매개변수 조정하는 방법
  - 그리드서치
요약
1. 교차 검증을 해야 함
  - 모델 학습: 훈련 데이터로
  - 모델과 매개변수 선택: 검증 데이터로
  - 모델 평가: 테스트 데이터로
  - 한 번 분리하는 것이 아니라 교차 검증으로 분할 반복
  - 훈련, 테스트로 분할 후, 모델과 모델 매개변수 선택을 위해 훈련 세트에 교차 검증 적용
2. 모델 선택과 평가에 사용하는 평가 지표와 방법이 중요함
  - 높은 정확도의 모델을 만드는데에서 끝나는 일은 없음
  - 이후 비즈니스에서 사용되는 상황을 잘 대변해야함
  - FP, FN이 매우 큰 영향을 미침, 이런 영향을 이해하고있어야함

교차 검증

데이터를 여러 번 반복해서 나누고, 여러 모델 학습
가장 널리 쓰이는 k-겹 교차 검증(k-fold cross-validation)
- 보통 5, 10을 사용

scikit-learn

  from sklearn.model_selection import cross_val_score
  from sklearn.linear_model import LogisticRegression

  iris = load_iris()
  logreg = LogisticRegression()

  scores = cross_val_score(logreg, iris['data'], iris['target'], cv=10)
  print('교차 검증 점수: {}'.format(scores))
  print('교차 검증 평균 점수: {:.3f}'.format(scores.mean()))

장점
- train_test_split()에서의 우연에 의한 요소를 줄일 수 있음
- 모델이 훈련 데이터에 얼마나 민감한 지 알 수 있음.
  - 가장 최악의 점수와 최고의 점수 비교하면 쉽게 파악 가능
단점
- 여러 모델을 만들어야하기 때문에 속도가 느리다
주의점
- 교차검증 알고리즘은 모델을 만들어주지는 않는다는점!
- 평가만 함

계층별 k-겹 교차 검증 및 그외 전략들(stratified k-fold cross validation)

그림과 같이 타깃값이 정렬되어있으면, 평가 시 문제 발생
cross_val_score에선 분류일 경우는 계층별 k-겹 교차 검증 사용 (회귀는 단순 K-fold)
- 폴드 안의 클래스 비율이 전체 클래스 비율과 같도록 나눔
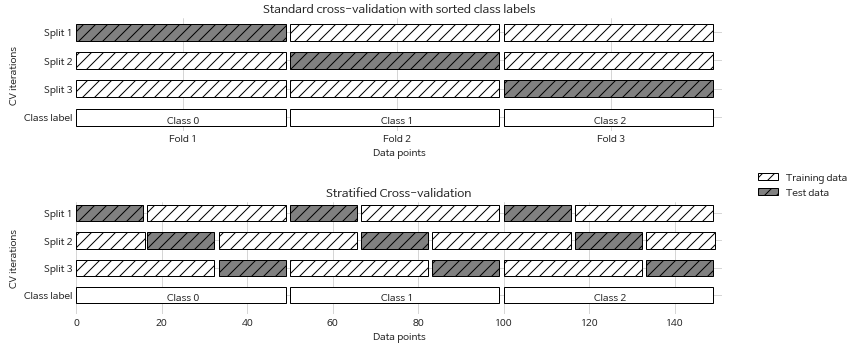
cv 매개변수에 교차 검증 분할기를 전달하여, 더 세밀하게 제어 가능
- shuffle=True, random_state 매개변수를 통해 교차 검증 분할기 조정
- 이후 cv에 전달하여 더욱 세밀한 제어
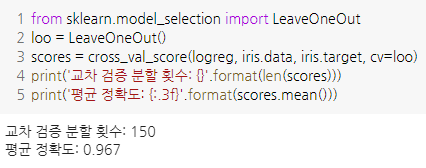
LOOCV(Leave-one-out cross-validation)
- k-겹 교차 검증에서 테스트 세트를 데이터 하나로 선택하는 것
- 큰 데이터 셋에선 오래 걸리지만, 작은 데이터 셋에선 효과적
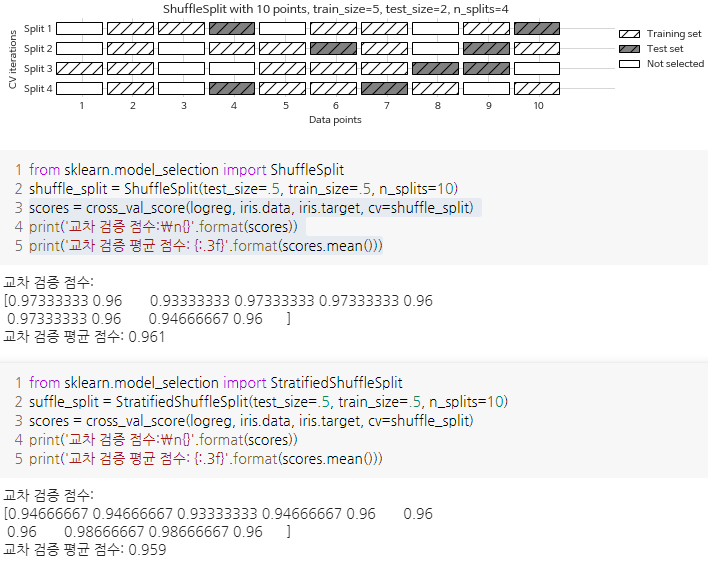
임의 분할 교차 검증(shuffle-split cross-validation)
- train_size, test_size만큼 분할하여 검증
- 매개변수
  - test_size, train_size: 정수를 입력하면 데이터 수, 실수 입력 시 비율
  - n_splits: 몇 번 진행할 지
- 분류에 더 적합한 StratifiedShuffleSplit 도 있음
- 이렇게 데이터를 부분 샘플링(subsampling)하는 방식은 대규모 데이터셋으로 작업 시 도움됨
그룹별 교차 검증
- 훈련 세트에 나온 그룹이 테스트 그룹에 나오지 않도록 조정
  - 클래스가 아니라 그룹!
  - ex. 의료데이터에서 환자 그룹(훈련: a, b, c환자 / 테스트: d, e환자)

그리드 서치

관심있는 매개변수들을 대상으로 가능한 모든 조합을 시도해보는 것
테스트 세트로 최적의 매개변수를 찾을 시, 모델의 성능을 테스트세트로 검증할 수 없음(이미 사용했으니)
따라서, 매개변수를 선택하는 세트를 나눠야함

검증 세트로 매개변수 선택
훈련 세트, 검증 세트로 모델 생성
- 데이터를 가능한 한 많이 활용하기 위해 두 폴드 사용(훈련 + 검증)

테스트 세트로 성능 확인

 # [훈련+검증], [테스트] 세트로 분할
 X_trainval, X_test, y_trainval, y_test =
 	train_test_split(iris.data, iris.target, random_state=0)
 # [훈련+검증] 세트 -> [훈련], [검증] 세트로 분할
 X_train, X_valid, y_train, y_valid =
 	train_test_split(X_trainval, y_trainval, random_state=1)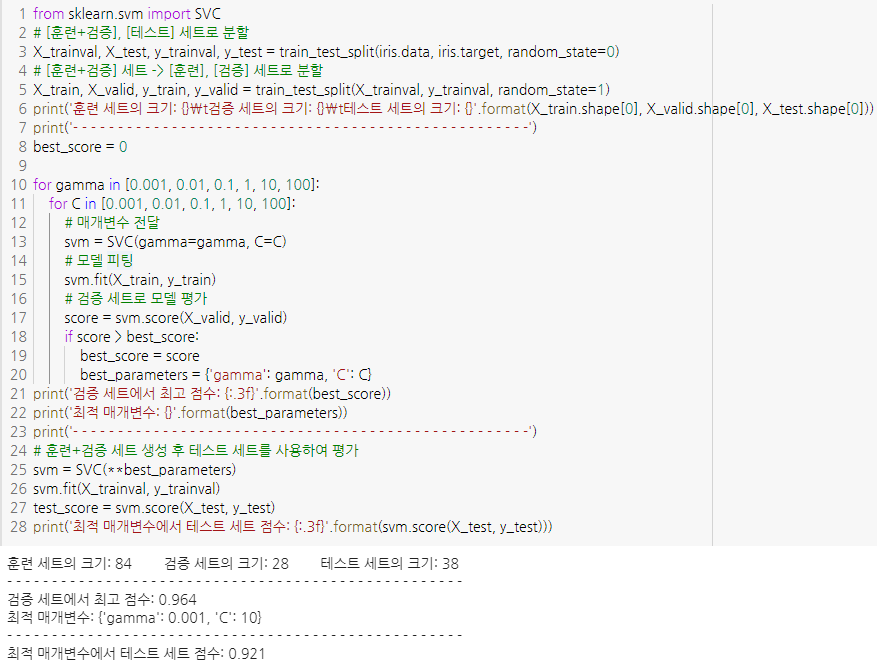

EDA, 모델 선택을 위해서는 훈련, 검증 세트를 사용하는 것 권장
테스트 세트를 사용하여 여러 모델을 평가하고 그 중 나은 것을 선택하는 것은 정확도를 낙관적으로 추정하는 것

교차 검증을 사용한 그리드 서치

매개변수도 훈련, 검증 세트를 여러 번 나눠서 교차 검증

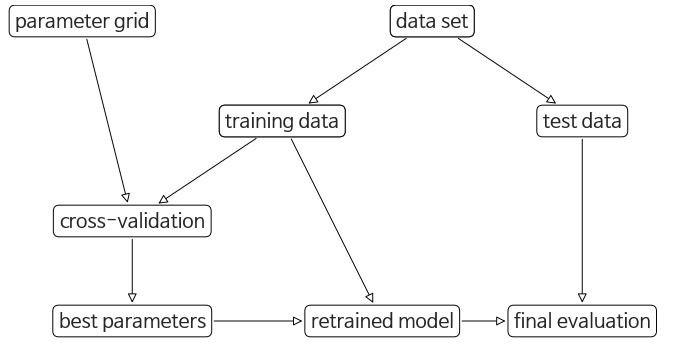
GridSearchCV 사용

  from sklearn.model_selection import GridSearchCV
  from sklearn.svm import SVC
  grid_search = GridSearchCV(SVC(), param_grid, cv=5)

  X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=0)

  grid_search.fit(X_train, y_train)

best_params_속성에 최적 매개변수, best_score_속성에 최상 교차 검증 점수 담김
GridSearchCV
- 테스트 세트 사용하지 않음
- 훈련 세트에서 알아서 검증 세트 분리
- 이후 내가 전달한 매개변수 그리드에서 최적의 매개변수 찾아냄
- train세트를 fit하고, test세트로 score 확인, best_score_, best_params_ 속성으로 매개변수, 점수 확인도 가능
- 연산 비용이 크므로, 간격을 넓게 하여 적은 수의 그리드로 시작하는 것이 좋음
  - 규제 매개변수처럼 연속형인 매개변수는 RandomizedSearchCV를 통해 확인하는 것도 좋음
  - RandomizedSearchCV는 주어진 범위에서 변수 무작위로 선택하여 조사
- 교차 검증 결과는 cv_results_속성에 저장되어있음
  - 저장된 결과가 많으므로, DataFrame으로 변환하여 보는 것이 좋음
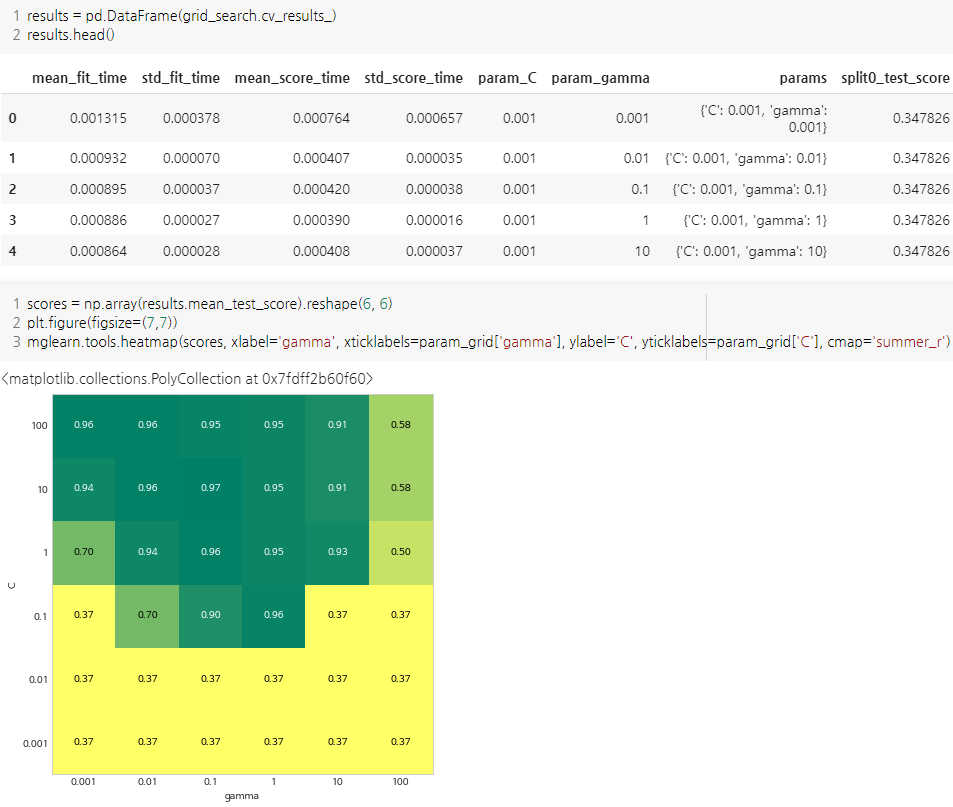
비대칭 매개변수 그리드 탐색
- ex. SVC모델
- ‘kernel’에 따라 입력되는 매개변수가 달라짐
  - linear: C, rbf: C, gamma …
- 이럴 때에는 딕셔너리로 매개변수 전달
그리드 서치에 다양한 교차 검증 적용
- 그리드 서치에서도 KFold 매서드를 활용할 수 있음
  - kfold = KFold(n_splits=1, ShuffleSplit=True)
  - grid_search = GridSearchCV(SVC(), param_grid, cv=kfold, return_train_score=True)
- 이런식으로 한 번만 분할하여 매우 큰 데이터셋에 활용해볼 수 있음

중첩 교차 검증

그리드 서치를 수행할 때 여전히 훈련, 테스트 데이터는 한 번만 나눔
한 번만 나누지 않고, 교차 검증 분할 방식을 사용 → 중첩 교차 검증
- 최적의 매개변수가 얼마나 잘 일반화되는가?

중첩 교차 검증은 주어진 모델이 얼마나 잘 일반화되는지 평가하는데 유용!

  param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
            'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
  scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5),
                       iris.data, iris.target, cv=5)
  print("교차 검증 점수: ", scores)
  print("교차 검증 평균 점수: {:.3f}".format(scores.mean()))
  print(param_grid)

교차 검증과 그리드 서치 병렬화
- n_jobs=-1을 통해 모든 코어를 활용한 병렬화 가능
- 하지만 병렬화를 중첩사용 불가
  - 모델에서 n_jobs 옵션 사용하면, 이 모델을 이용하는 GridSearchCV에서는 사용 불가

평가 지표와 측정

지금까지는 분류는 정확도, 회귀는 R²값을 사용했음

지도 학습 모델의 성능을 잴 수 있는 다른 지표들은 뭐가 있을까?

이진 분류의 평가 지표

가장 널리 사용되고 개념도 쉬운 이진 분류 알고리즘
핵심은 음성, 양성 클래스 중 무엇이냐

에러의 종류
- 1종 오류, 거짓 양성, 타입 1 에러
  - class 0인데 1로 구분
- 2종 오류, 거짓 음성, 타입 2 에러
  - class 1인데 0으로 구분
불균형 데이터셋(imbalanced datasets)
- 두 클래스의 비율이 매우 상이한 것
- ex. 100번의 광고 중 1번의 클릭 → (1, 99)로 불균형
- 이런 모델에서 99% 정확도로 예측하는 모델이 있다고 가정해보자
  - 모두 클릭 안함으로 구별하면 → 99% 정확도
  - 실제 99%로 예측해도 → 99% 정확도
  - 이런 상황을 잘 구분해야함

오차 행렬(confusion matrix)

이진 분류 평가 결과를 나타낼 때 널리 사용되는 방법 중 하나
대각 행렬이 제대로 분류한 것
- TN: 진짜 음성, TP: 진짜 양성 이라고도 함
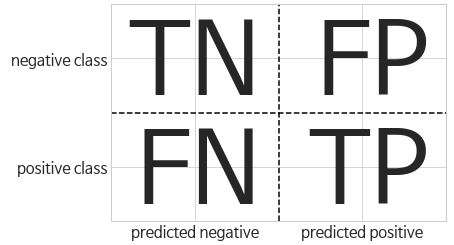
하지만 전체 오차 행렬을 매번 조사하기는 번거로움
이를 요약해서 알 수 있는 방법은 없을까?
- 그 전에, 정확도와의 관계를 살펴보자
정확도와의 관계
- 정확도는 TP + TN / TP + TN + FP + TN
- 전체 중 맞춘 클래스의 수

정밀도(precision), 재현율(recall), f-점수

정밀도
- 양성으로 예측된 것 중 진짜 양성(TP)
- TP / TP + NP
- 거짓 양성의 수를 줄이는 것이 목표일 때 성능 지표로 사용
- 예시
  - 임상 실험은 비싸서 단 한 번의 실험으로 효과를 검증하고 싶음
  - 거짓 양성을 줄이는 것이 중요함
- PPV라고도 함
재현율
- 전체 양성 샘플 중 실제로 얼마나 진짜 양성으로 분류되었는지?
- TP / TP + NF
- 모든 양성 샘플을 식별해야 할 때, 거짓 음성(FN)을 피하는 것이 중요할 때 사용
- 예시
  - 암 환자를 진단할 때는 FP가 나오더라도 FN가 안나오는 것이 중요
- 민감도(sensitivity), 적중률(hit rate), 진짜 양성 비율(TPR) 이라고도 함
정밀도와 재현율은 서로 상충
- 모두 음성으로 예측하면, 재현율은 높지만 정밀도는 낮아짐
f₁-점수(f₁-score) 또는 f₁-측정(f₁-measure)
- 정밀도와 재현율 둘 중 하나만 가지고는 전체 그림을 보기 어려움
- 정밀도와 재현율의 조화평균으로 나타낸 것이 f-점수
  - 2 * (정밀도 * 재현율) / (정밀도 + 재현율)
  - 이 공식을 f₁-점수 라고도 한다
- f1_score로 조회 가능
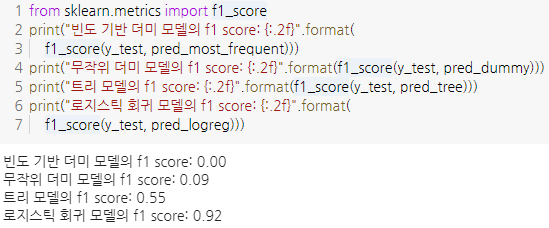
- classification_report로 정밀도, 재현율, f1점수를 한 번에 출력도 가능
불확실성 고려
- decision_function_에서 원래는 임계값이 0 이상이면 양성 클래스, 음수면 음성 클래스로 분류함
- 근데 재현율을 높이는 것이 중요하다면, 임계값을 낮춰서 더 많이 양성 클래스로 분류해야함
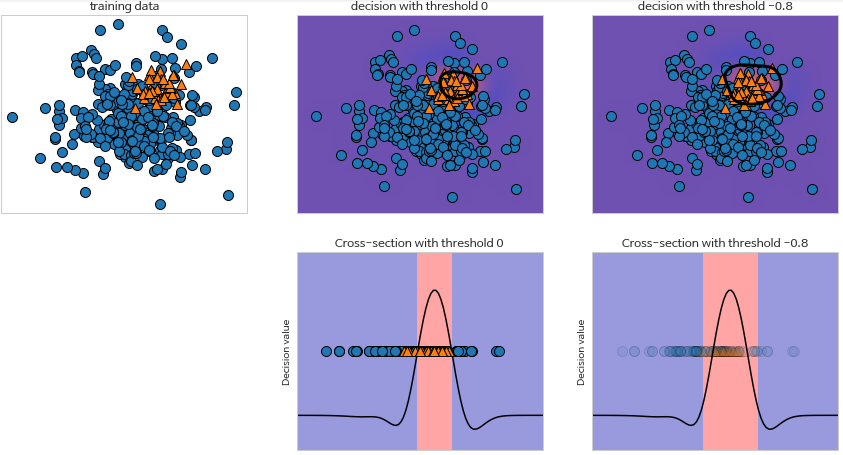
```
  # 실습을 위해 test세트 이용, 실전에선 안돼!
  y_pred_lower_threshold = svc.decision_function(X_test) > -.8
```
- predict_proba는 출력이 0~1 사이이므로 임계값 변경 기준을 찾기가 보다 쉬움
  - 기본값이 0.5인데, 이를 더 높이면 양성 클래스로 분류하기 위해 더 많은 확신이 있어야함
- 모든 모델이 쓸모있는 불확실성을 제공하는 것은 아님, 보정과 깊게 관련있음
  - 보정된 모델은 불확실성을 정확하게 측정하는 모델
  - 이후 더 알아야한다면 추가 자료 공부
정밀도-재현율 곡선과 ROC곡선
- 임계값을 조정하는 것은 정밀도와 재현율의 상충 관계를 조절하는 것
  - 90% 이상의 재현율을 얻기 위해 100% 재현율이 되도록 임계값 조정
  - →정밀도가 0으로 나오면 무쓸모됨
- 90% 재현율 처럼 필요조건(목표)를 지정하는 것을 운영 포인트를 지정한다고 함(operating point)
- 운영 포인트가 명확하기 않은 경우가 많음
  - 이럴 때에는 모든 임계값을 조사해보거나
  - 한 번에 정밀도나 재현율의 모든 장단점을 살펴보는 것이 좋음
- 이를 위해서 정밀도-재현율 곡선을 사용함(precision-recall curve)
  - 타겟 레이블과 decision_function 혹은 predict_proba 메서드로 계산한 예측 불확실성 이용
  - 재현율을 높게 유지하며 정밀도도 높게 유지할 수 있으면 최고!
    - 곡선이 오른쪽 위로 가면 갈 수록 좋음
    - 임계값은 제일 낮은 왼쪽 위부터 시작함
  - decision_function을 지원하지 않는 랜덤포레스트의 경우, predict_proba[:, 1]로 측정
    - 양성 클래스가 될 확률
  - 재현율이 높거나 정밀도가 높은 극단적인 양 끝은 rf이 높으나, 중간은 svc가 더 좋음
  - f1점수만 보면 이런 세세한 부분 놓칠 수 있음
    - f1점수는 정밀도-재현율 곡선의 한 지점인 기본 임계값에 대한 점수
  - 이렇게 곡선을 비교하면 인사이트를 많이 얻을 수는 있지만, 수작업이고 번거로움
    - 이를 요약, 비교하기 위해 정밀도-재현율 곡선의 아랫부분 면적을 계산
    - 이를 평균 정밀도(average precision)이라고 함
    - average_precision_score 함수에서 제공
- ROC와 AUC
  - ROC 곡선
    - 여러 임계값에서 분류기의 특성을 분석하는 데 쓰이는 도구
    - 정밀도, 재현율 대신, 진짜 양성 비율(TPR)에 대한 거짓 양성 비율(FPR)을 나타냄
    - FPR = FP / FP + TN
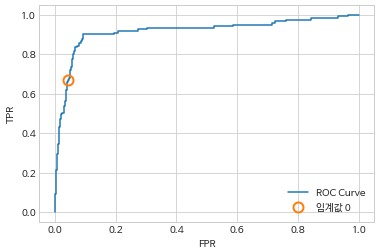
    - ROC곡선은 왼쪽 위에 가까울수록 이상적
    - 평균정밀도처럼 ROC곡선 아래의 면적값 하나로 ROC 곡선을 요약 가능
    - 이 면적을 AUC(area under the curve)라고 하며, roc_auc_score 함수로 계산
    - 불균형한 클래스를 분류하는 문제에서 모델 선택 시, 정확도보다 AUC가 훨씬 의미있는 정보 제공
      - 무작위로 분류할 시, TPR과 FPR의 비율이 비슷해지며 ROC곡선은 y=x와 비슷해지고, AUC면적은 0.5가 됨

다중 분류의 평가 지표

기본적으로 이진 분류에서 유도된 것이며, 클래스에 대해 평균을 낸 것
다중 분류에서 불균형 데이터셋을 위해 가장 널리 사용한 평가 지표는 f1-점수의 다중 분류 버전
- average 매개변수를 사용하여 지원하며, 기본값은 binary
  - macro: 클래스별 f1-점수에 가중치 주지 않음. 클래스 크기에 상관없이 모든 클래스를 같은 비중으로 다룸. 각 클래스를 동일한 비중으로 고려한다면 추천
  - weighted: 샘플별로 가중치를 두어 평균 계산.
  - micro: 모든 클래스의 FP, FN, TP의 총 수를 헤아린 후, 정밀도, 재현율, f1-점수를 이 수치로 계산. 각 샘플을 똑같이 간주한다면 추천

회귀의 평가 지표

회귀도 분류처럼 타깃을 과대 예측한 것 대비 과소 예측한 것 분석 가능.
하지만 대부분 R스퀘어 값으로 충분
MSE(평균제곱오차), MAE(평균절대오차) 사용하여 모델을 튜닝할 때 이런 지표 기반으로 비즈니스 결정 가능
하지만 일반적으로 R스퀘어가 더 나음

모델 선택에서 평가 지표 사용하기

그리드서치나, 교차검증 사용하여 모델 선택 시, AUC같은 평가 지표를 사용하고자 하는 경우가 있음
이럴 때에는 GridSearchCV와 cross_val_score의 scoring 매개변수를 통해 손쉽게 구현 가능!
분류 문제에서 scoring 매개변수의 중요한 옵션
- accuracy
- roc_auc
- average_precision
- 이진f1-점수인 f1
- 가중치 방식에 따라 f1_macro, f1_micro, f1_weighted
회귀에서 널리 사용하는 것
- r2
- mean_squared_error
- mean_absolute_error

서울숲 미세먼지

모델 평가와 성능 향상 스터디 내용 요약

5. 모델 평가와 성능 향상

교차 검증

그리드 서치

평가 지표와 측정

댓글남기기

참고

실무를 위한 ABtest Study

글또 5기 후기

그래서 무슨 지표를 보라는걸까

dump를 알기 전까지 한 모든 삽질