word2vec이란?

업데이트: January 10, 2021

3. word2vec

3.1. 추론 기반 기법과 신경망

분포 가설을 복습해보자. 분포 가설은 ‘단어의 의미는 그 주변 단어(맥락)에 의해 정해진다’라는 개념이다. 단어를 벡터로 표현하는 방법은, 크게 ‘통계 기반 기법’과 ‘추론 기반 기법’이 있는데, 이 두 방법들은 모두 이 분포 가설을 배경으로 한다. 추론 기반 기법을 살펴보기 전, 통계 기반 기법의 문제점을 살펴보자.

3.1.1. 통계 기반 기법의 문제점

통계 기반 기법에서는 단어의 동시발행과 PPMI행렬 등을 만들고, 이에 SVD를 적용한다. SVD의 계산 복잡도는 $O(n^3)$인데, 어휘가 100만개 등으로 많아진다면 현실적으로 계산이 불가능해진다. 속도를 개선시킬 수 있다 하더라도 많은 컴퓨팅파워가 필요하다.

한편, 추론 기반 기법에서는 1회 만에 데이터를 처리하지 않는다.(통계 기반의 SVD처럼) 미니배치로 학습시키며 가중치를 개선해나간다. 데이터를 작게 나눠서 학습시키므로, 큰 데이터에서도 잘 적용된다. 또한 GPU를 통한 병렬 계산도 가능하여 속도를 많이 개선시킬 수 있다.

3.1.2. 추론 기반 기법 개요

추론 기반 기법에선 맥락이 주어졌을 때, 어떤 단어가 들어가는지 추측, 추론하는 것이 주된 작업이다.

예를들면…

You ? goodbye and I say hello 에서 ?에 무엇이 들어가는지 추측하는 것!
- 모델은 위 추론 문제를 계속 학습하게 된다.
- 모델은 ?에 들어갈 각 단어의 출현 확률을 출력한다.

3.1.3. 신경망에서의 단어 처리

신경망에 단어를 넣을 때, you, say 등을 그대로 넣을 수 없으니, 이를 one-hot표현으로 변환한다.

You say goodbye and I say hello. 를 one-hot 표현으로 바꾸면
- id = {0 : ‘you’, 1 : ‘say’, 2 : ‘goodbye’, 3 : ‘and’, 4 : ‘i’, 5 : ‘hello’, 6 : ‘.’}
- you: [1, 0, 0, 0, 0, 0, 0]
- say: [0, 1, 0, 0, 0, 0, 0]

각 단어들을 one-hot-벡터로 표현하면, 신경망을 구성하는 레이어들에서 벡터를 처리할 수 있다.(=단어를 신경망으로 처리할 수 있게 된다.)

요런식으로!
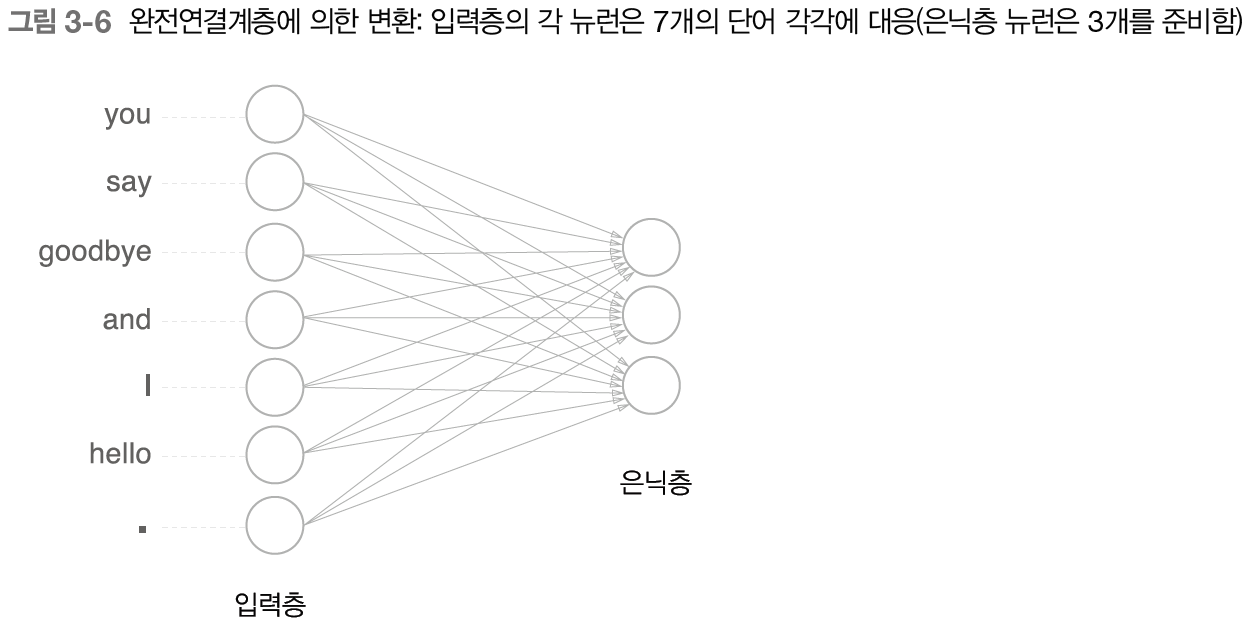
- 위 이미지는 편향은 생략되었으며, 각 화살표들에는 가중치가 존재한다.

3.2. 단순한 word2vec

word2vec에서 제안하는 CBOW(continuous bag-of-words) 모델을 살펴보자.

3.2.1. CBOW 모델의 추론 처리

CBOW 모델은 맥락으로부터 원하는 타겟을 추측하는 용도로 사용되는 신경망이다. 여기서 타겟은 중앙 단어이며, 맥락은 타겟 주변의 단어들이다. CBOW 모델의 input은 one-hot 표현 된 맥락이다.

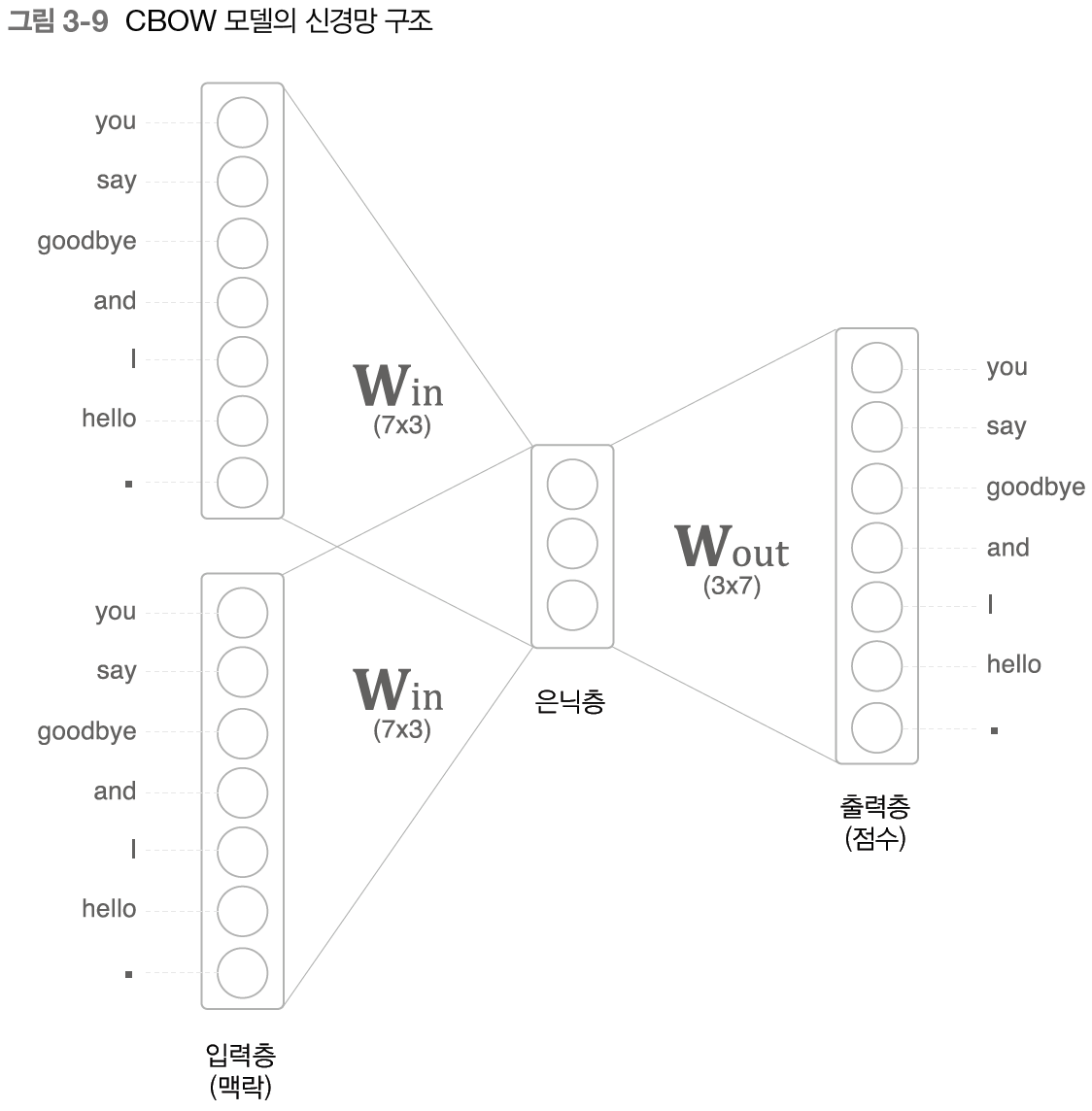
/assets/images/DLscratch2/3/fig_3-9.png

위 그림에서 input layer가 2개인 이유는 맥락으로 고려할 단어가 2개로 정했기 때문이다. 예를들어, say라는 단어가 타겟이라면 input1은 you, input2는 goodbye에 대한 onehot 벡터일 것이다. input은 $\mathbf{W}_{\text{in}}$가중치로 완전연결계층을 거쳐 은닉층으로 변환된다.

여기서 $\mathbf{W_{\text{in}}}$가중치가 단어의 분산 표현이다.
- 분산 표현을 쉽게 설명하면, ‘빨간색’ 을 RGB값인 (255, 0, 0)으로 표현한 것과 유사하게, 각 단어들을 표현해낸 것
- 학습을 진행하며 이 분산 표현이 단어를 잘 추측할 수 있도록 갱신된다. 그리고 단어의 의미도 잘 녹아든다.

이 과정에서 input1과 input2에서 각각 2개의 값이 전달되는데, 은닉층 뉴런은 이 값들을(여기선 두 값) 평균낸다.

은닉층에서 $\mathbf{W}_{\text{out}}$가중치로 완전연결계층이 처리되며 출력층으로 전달된다. 이 출력층엔 각 단어의 점수를 뜻하게된다. 점수가 높다면, 대응 단어의 출현 확률이 높다는 것을 의미한다. 주의할 점은 이 점수는 확률은 아니며, 확률로 표현하기 위해선 Softmax계층을 거치면 된다.

핵심은, 은닉층의 뉴런 수를 입력층의 뉴런 수보다 적게 하는 것이다.
- 그래야 은닉층에 필요한 정보를 간결하게 담을 수 있고,
- 밀집벡터 표현을 얻을 수 있다. (input데이터는 one-hot 표현이다보니 sparse한 데이터)

계산 그래프로 표현하면 아래 그림처럼 나타내진다.

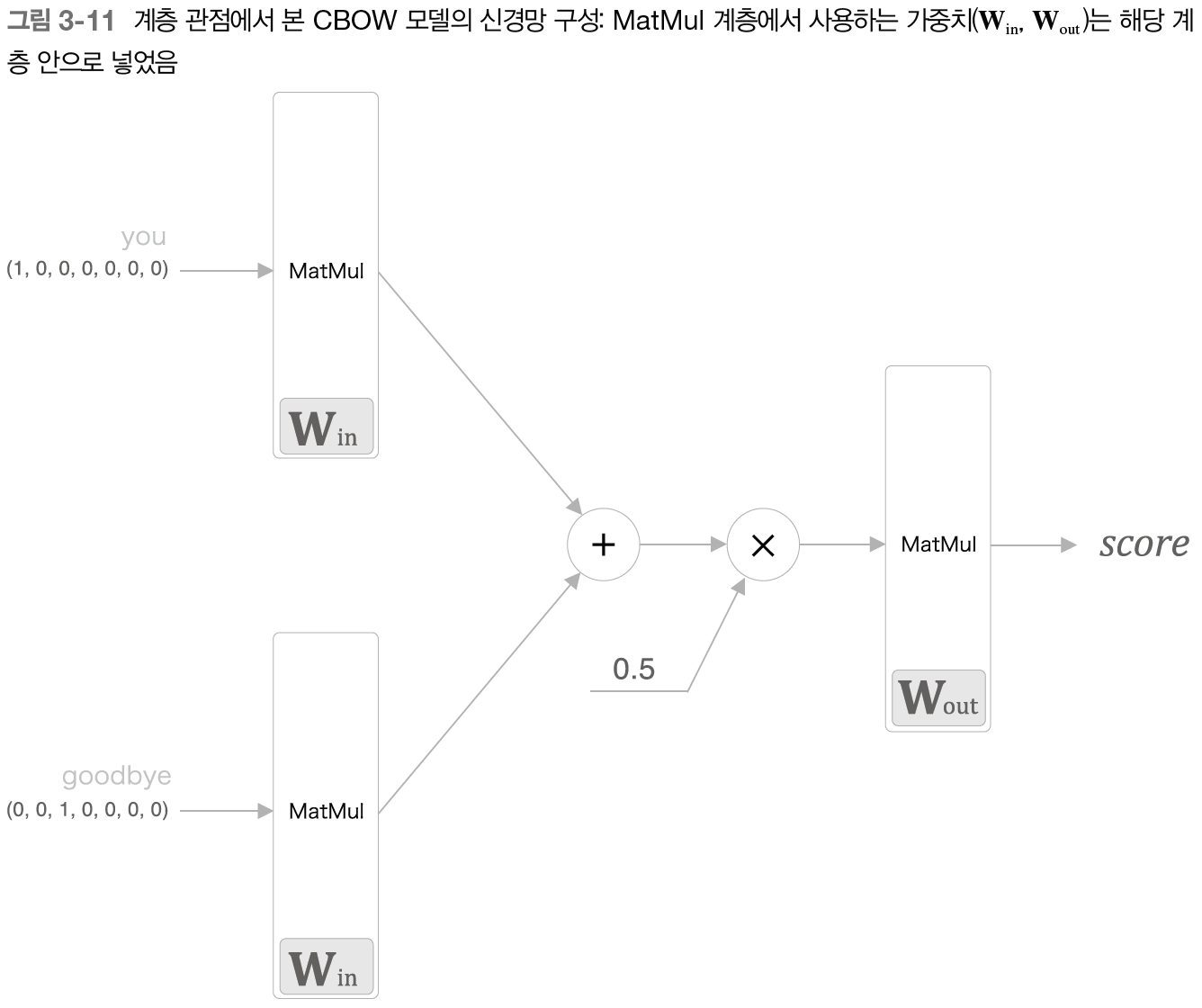
/assets/images/DLscratch2/3/fig_3-11.png

0.5가 곱해지는 노드는 평균을 구하기 위해 곱해지는 것!

CBOW 모델은 활성화 함수를 사용하지 않고 간단하게 구성된 신경망이다. 여러 입력층(맥락 수에 따른)이 존재하고, 이 입력층들이 하나의 가중치를($\mathbf{W}_{\text{in}}$)공유한다는 특징이 있다.

3.2.2. CBOW 모델의 학습

CBOW모델의 학습에서는 가중치들이 조정되며 단어의 출현 패턴을 파악한 벡터가 학습된다. 그리고 CBOW모델은 사용한 데이터 말뭉치를 통해 학습하므로, 다른 말뭉치를 사용하면 같은 단어라도 분산 표현이 달라진다. 예를 들어, ‘스포츠’ 기사를 사용하는 경우와 ‘연예’ 기사를 사용하는 경우, 같은 단어라도 분산 표현이 달라질 것이다.

그리고 위 계산 그래프에는 포함되지 않았지만, 다중 분류이므로, 소프트맥스 계층에서 나오는 확률들을 통해 cross entropy loss를 계산하여 학습을 진행한다.

(참고) Cross entropy loss 수식
- $E=-\sum_k{t_k\log{y_k}}$

3.2.3. word2vec의 가중치와 분산 표현

위에서 살펴본 것처럼, word2vec에는 두 가지의 가중치가 존재한다.

input layer와 hidden layer 사이의 $\mathbf{W}_\text{in}$
hidden layer와 output layer 사이의 $\mathbf{W}_\text{out}$

이 두 가중치 중 어떤 것을 분산 표현으로 선택해야할까? 혹은 둘 다 선택해야할까?

word2vec, 특히 skip-gram모델에서는 첫 번째인 $\mathbf{W}_\text{in}$만 분산 표현으로 선택한다고 한다.

3.3 word2vec 보충

지금까지는 CBOW의 구조에 대해서 알아봤는데, 이번에는 확률 관점에서 다시 살펴보자. (근데 이 부분은 일단 정리는 해두는데, 완벽하게 이해가 가지는 않았다. 나중에 더 공부하기..)

3.3.1 CBOW 모델과 확률

$w_\text{1}, w_\text{2}, \cdots, w_\text{t-2}, w_\text{t-1}, w_\text{t}, w_\text{t+1}, w_\text{t+2}, \cdots$와 같은 말뭉치가 있고, $w_\text{t-1}, w_\text{t+1}$이 맥락으로 주어졌다고 가정해보자.

다시 표현하면 $w_\text{t-1},w_\text{t+1}$가 일어난 후 $w_\text{t}$가 발생할 확률을 구하는 것이므로,
$\text{P}(w_{\text{t}}\mid{}w_{\text{t-1}},w_{\text{t+1}})$로 표현할 수 있다.
즉 CBOW모델은 위 식을 모델링하고 있는 것이다.

그럼 이 관점에서 CBOW의 loss function도 표현해보자.

cross entropy loss의 수식은 $E=-\sum_k{t_k\log{y_k}}$다. 여기서 $t_k$는 정답 레이블이고 one-hot 벡터이므로, 실제 정답 레이블을 제외하면 모두 0이다. 실질적으론 정답 레이블에 대한 로그값을 구하는 것이다.

$\text{L}=-\log{P(w_{t}\mid{}w_{t-1},w_{t+1})}$로 loss의 식을 간편하게 표현할 수 있다. 사실 CBOW가 모델링하고 있는 식에 log를 씌운 후, 음수를 취하면 된다. 이것을 음의 로그 가능도(negative log likelihood)라고 한다.

식을 간단히 설명하면 타겟을 바꿔가며 loss를 구하고 이를 평균내는 것
확률 관점에서 어떻게 표현했는지를 참고하여 공부하기

3.3.2 skip-gram 모델

CBOW 모델은 타겟 단어 주변의 맥락을 알려주고, 타겟이 어떤 단어일지 예측한다. 예를 들어, ‘I’, ‘you’라는 단어를 주고 , 그 가운데에 무슨 단어가 들어갈 지 맞추는 식이다. skip-gram 모델은 이와 반대로, 단어 하나가 주어지면 그 주변에 어떤 단어가 올 지에 대한 문제를 푸는 모델이다.

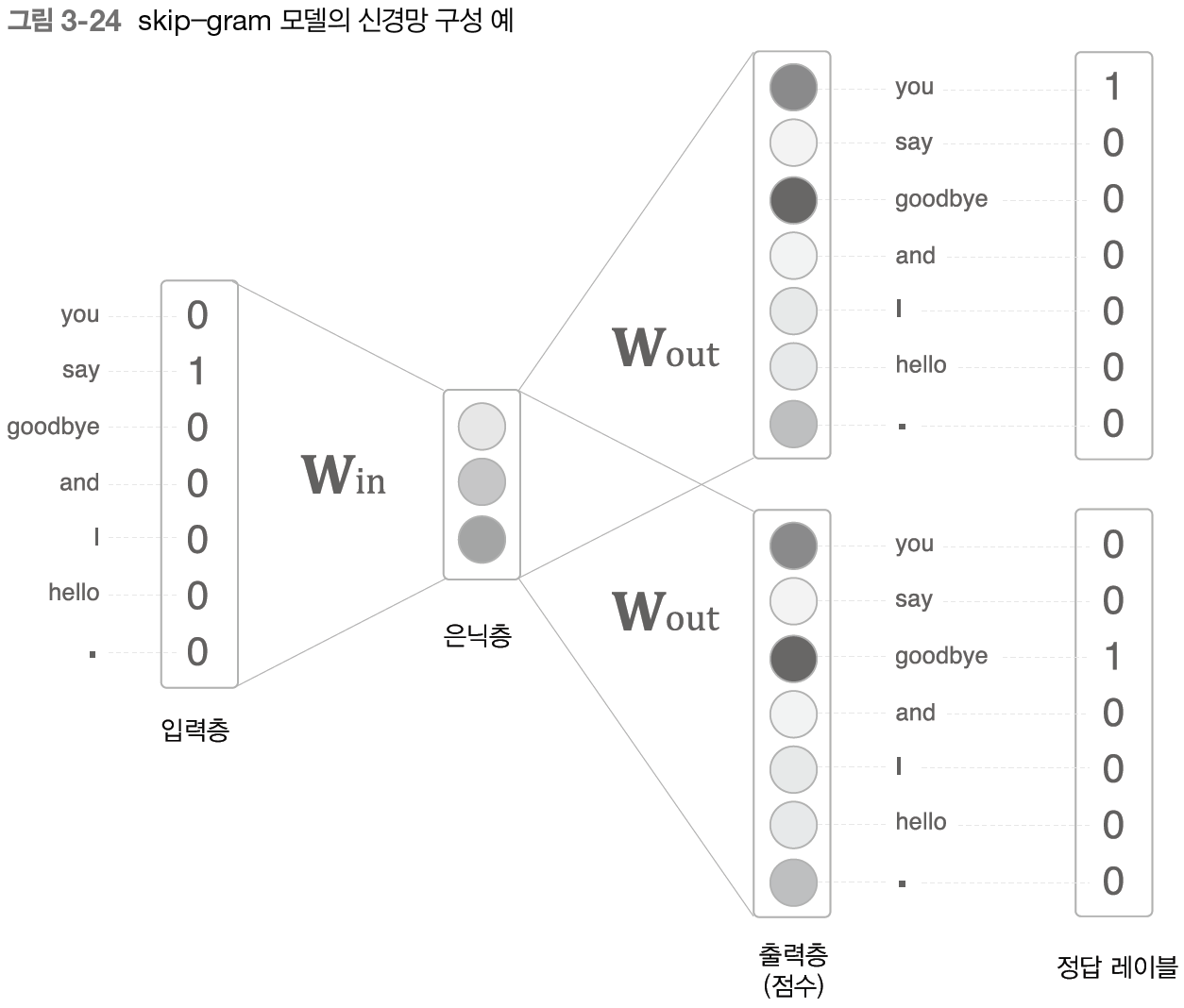
/assets/images/DLscratch2/3/fig_3-24.png

skip-gram의 모델의 Input layer은 하나이며, CBOW와 반대로 output layer가 여러개이다. (맥락의 수 만큼) 각 output layer에서는 개별적으로 loss를 구하고, 이 손실들을 모두 더한 값이 최종 loss다.

이 모델도 확률로 표현해보면, $P(w_{t-1},w_{t+1}\mid{}w_{t})$가 된다. skip-gram 모델에선 각 맥락의 단어들이 조건부 독립이라는 가정 하에 위 식을 분리한다.

$P(w_{t-1},w_{t+1}\mid{}w) = P(w_{t-1}\mid{}w_t)P(w_{t+1}\mid{}w_{t})$ 요렇게!

이제 skip-gram의 식에서 cross entropy loss를 구하는 식을 구하면, 아래와 같다.

$L = -\log{P(w_{t-1}, w_{t+1}\mid{}w_t}) = -\log{P(w_{t-1}\mid{}w_t)P({w_{t+1}}\mid{}w_t}) = -\log{P(w_{t-1}\mid{}w_t) + \log{P({w_{t+1}}\mid{}w_t})}$
- $\log{xy} = \log{x}+\log{y}$에서 유도

이제 어려운 얘기는 그만하고, CBOW와 skip-gram가 푸는 문제를 사람이 푼다고 생각해보자.

CBOW: I랑 you가 있어. 그 사이에 어떤 단어가 들어갈 수 있겠니?
- 나: 동사가 들어가지 않을까? 근데 소설 맥락 상 love일 것 같아.
skip-gram: you라는 단어가 있어. 그 앞뒤에 어떤 단어가 올 것 같아?
- 나: ????

이처럼 skip-gram은 CBOW보다 더 복잡한 문제를 풀어낸다. 더 복잡하고 어려운 문제에 도전하는 만큼, 각 단어의 분산 표현은 오히려 더 뛰어날 가능성이 있는 것이다.

그러면 과연 어떤 모델을 써야할까?

책에서는 CBOW대신 skip-gram 사용을 권장하고 있다. 이유는 당연히 성능이 더 좋기 때문이다. 특히 말뭉치가 커질수록 저빈도 단어나 유추 문제 성능 면에서 skip-gram모델이 더 뛰어나다고 한다.

다만, skip-gram은 output laye에서 loss를 맥락의 수만큼 (위 예시는 2였지만 더 많아진다면?!)구해야 하기 때문에, 계산 비용이 더 커진다는 단점이 존재한다.

3.3.3 통계 기반 vs 추론 기반

앞서 공부한 통계 기반 기법과 이번에 공부한 추론 기반 기법을 비교해보자.

통계 기반 기법은 말뭉치의 전체 통계를 단 1번의 학습만으로 단어의 분산 표현을 얻어낸다. 추론 기반 기법은 미니배치 학습으로, 말뭉치를 일부분식 학습한다.

통계 기반 기법은 새로운 데이터 갱신이나 수정 등에 어려움이 있다. 추론 기반 기법은 새로운 데이터 추가가 용이하다. 가장 마지막에 학습시킨 파라미터로 추가된 말뭉치들을 학습시키면 된다.

이렇게 놓고보면 추론 기반 기법이 성능면에서도 우월할 것으로 보이지만, 실제로는 이 두 기법의 우열을 가릴 수 없었다고 한다. 그리고 최근 GloVe이라는 기법이 등장했는데, 이 기법은 추론 기반 기법과 통계 기반 기법을 융합한 것이라고 한다!

요약

추론 기반 기법은 추측이 목적이고, 단어의 분산 표현을 얻을 수 있다. (가중치)
word2vec은 추론 기반 기법이고, 2층 신경망이다.
- CBOW, skip-gram모델이 있다.
CBOW모델은 맥락으로부터 타겟을 추측하고, skip-gram은 단어로부터 그 주변 단어(맥락)을 추측한다.
- skip-gram이 더 성능이 좋다.
word2vec은 가중치를 다시 학습시킬 수 있으므로, 새로운 데이터(말뭉치)에 대해 쉽게 업데이트가 가능하다.

서울숲 미세먼지