오차역전파법이란?
업데이트:
5. 오차역전파법
- 수치 미분은 간단하지만 시간이 오래걸린다는 단점이 있다.
- 이번에는 가중치 매개변수의 기울기를 효율적으로 계산하는 오차역전파(backpropagation)을 살펴보자.
5.1 계산 그래프
- computational graph
- 계산 과정을 그래프로 나타낸 것 (그래프 자료구조)
- 복수의 노드(node)와 에지(edge)로 표현
5.1.1 계산 그래프로 풀다
-
1개에 100원인 사과 2개를 샀다. 소비세가 10%일 때, 지불 가격을 구하자.

- 계산 과정을 노드와 화살표로 표현한다.
- 노드는 원으로 표기하고, 원 안에 연산 내용을 적는다.
- 계산 과정을 노드와 화살표로 표현한다.
-
사과 개수와 소비세를 변수라고 생각하여 풀면 아래와 같이 표현할 수 있다.
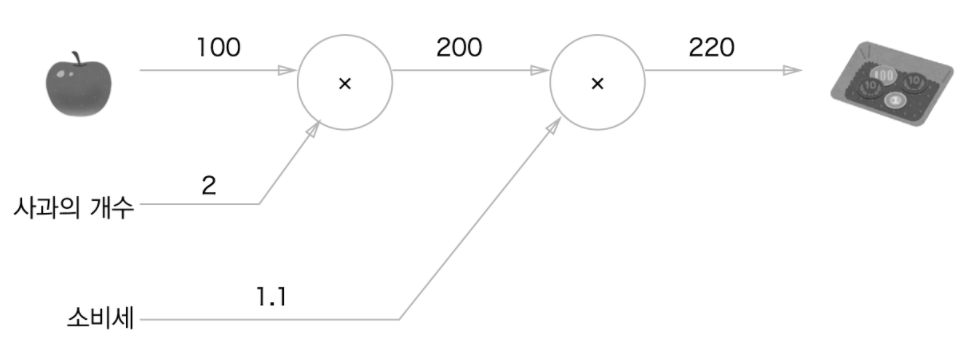
-
이번에는, 100원짜리 사과와 150원짜리 귤을 각각 2, 3개씩 샀다고 해보자.
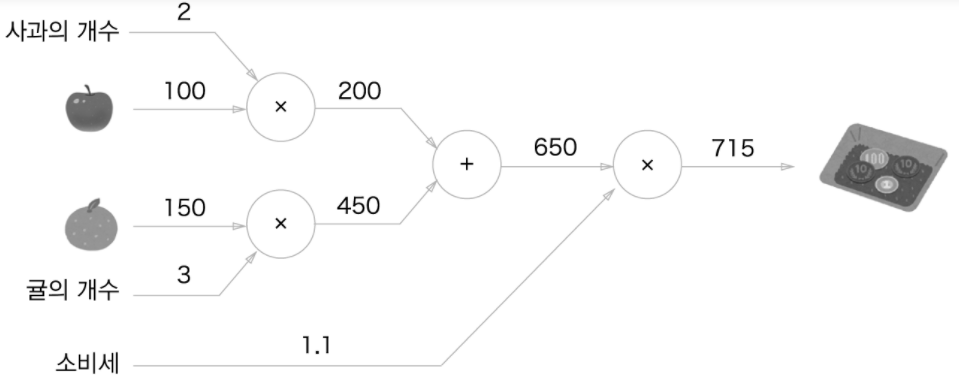
- 위의 그래프와 달리, 덧셈 노드가 등장하며 두 금액을 합산해준다.
-
그래프를 통한 문제 풀이의 흐름을 정리해보자.
- 계산 그래프를 구성한다.
- 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다.
- 이 단계를 순전파(forward propagation)라고 한다.
- 순전파는 계산 그래프의 출발점으로부터 종착점으로의 전파이다.
- 반대 방향의 전파는 역전파(backward propagation)라고 한다.
5.1.2 국소적 계산
- 계산 그래프의 특징은, 국소적 계산을 전파함으로써 결과를 전달한다는 것이다.
- 국소적 계산이란,
- 자신과 직접 관계된 작은 범위만 계산한다는 의미로,
- 어떤 일이 벌어지든 자신과 관계된 정보만으로 결과를 출력할 수 있다는 것이다.
- 국소적 계산이란,
- 계산 과정이 아무리 복잡하더라도 각 노드에서 하는 계산은 ‘국소적 계산’이다.
- 국소적 계산은 단순하지만, 결과를 전달함으로써 전체를 구성하는 복잡한 계산을 해낼 수 있다.
5.1.3 왜 계산 그래프로 풀까?
- 계산 그래프의 장점은 무엇일까?
- 국소적 계산
- 복잡한 계산이라도, 각 노드에서는 문제를 단순화할 수 있다.
- 중간 계산 결과를 모두 보관할 수 있다.
- 위 문제에서는, 사과 2개를 계산하면 200원, 소비세를 더하기 전 금액은 650원 …
- 역전파를 통해 ‘미분’을 효율적으로 계산할 수 있다.
- 국소적 계산
- 다시 위의 문제로 살펴보자 (사과 2개를 사서 소비세를 포함한 금액을 구하는 문제)
- 여기서 사과 가격이 오르면 최종 금액에 어떤 영향을 끼칠까?
- → ‘이는 사과 가격에 대한 지불 금액의 미분’을 구하는 문제로 볼 수 있다.
- 사과 값을 $x$, 지불 금액을 $L$이라 하면, $\frac{\partial L}{\partial x}$를 구하는 것이다.
- 사과 가격이 아주 조금 올랐을 때, 지불 금액이 얼마나 증가하는지?
-
이는 역전파를 하면 구할 수 있다.
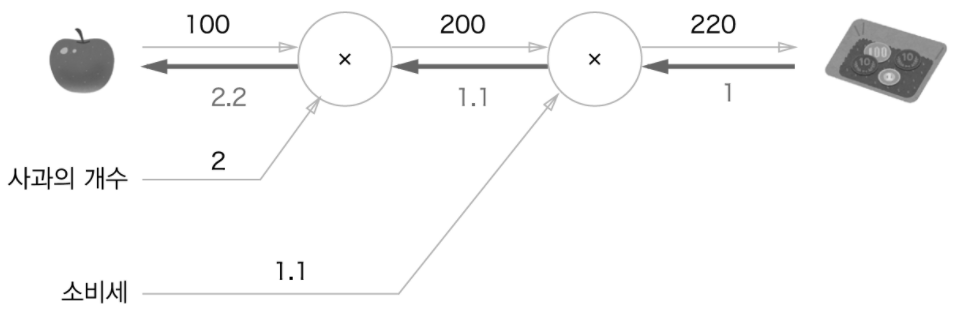
- 굵은 화살표가 역전파이며, 이 전파는 ‘국소적 미분’을 전달한다.
- 따라서 사과 가격에 대한 지불 금액의 미분값은 2.2로,
- 사과 가격이 아주 조금 오르면, 지불 금액은 그 2.2배가 오른다는 의미
- 따라서 사과 가격에 대한 지불 금액의 미분값은 2.2로,
- 굵은 화살표가 역전파이며, 이 전파는 ‘국소적 미분’을 전달한다.
5.2 연쇄법칙
- 역전파는 ‘국소적인 미분’을 순방향과는 반대인 오른쪽에서 왼쪽으로 전달한다.
- 이렇게 전달하는 원리는 연쇄법칙(chain rule)에 따른 것인데, 이에 대해 자세히 알아보자.
5.2.1 계산 그래프의 역전파
-
$y=f(x)$라는 계산의 역전파를 그려보자.
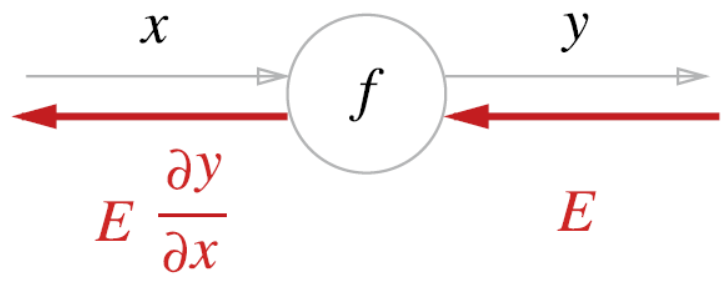
- 신호 $E$에 노드의 국소적 미분인 $\frac{\partial y}{\partial x}$를 곱한 후, 다음 노드로 전달한다.
- 여기서 국소적 미분은 순전파때의 $y=f(x)$의 미분을 구한다는 것이며,
- $x$에 대한 $y$의 미분을 구한다는 뜻이다.
- 신호 $E$에 노드의 국소적 미분인 $\frac{\partial y}{\partial x}$를 곱한 후, 다음 노드로 전달한다.
-
위 방식과 연쇄법칙의 원리가 합쳐지면 목표로 하는 미분 값을 효율적으로 구할 수 있다.
5.2.2 연쇄법칙이란?
- 연쇄법칙 이전에, 합성 함수에 대해 알아보자.
- 합성 함수란, 여러 함수로 구성된 함수이다. (아래에 예시 참고)
- $z=t^2$
- $t=x+y$
- 합성 함수란, 여러 함수로 구성된 함수이다. (아래에 예시 참고)
- 연쇄법칙은 함성 함수의 미분에 대한 성질이며, 아래와 같이 정의된다.
- 함성 함수의 미분은 함성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
- 위의 $z$에 대한 식으로 이를 설명하자면,
- $\frac{\partial z}{\partial x}$($x$에 대한 $z$의 미분)은 $\frac{\partial z}{\partial t}$와 $\frac{\partial t}{\partial x}$의 곱으로 나타낼 수 있다.
- $\frac{\partial z}{\partial x}=\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$로 나타낼 수 있는데, 약분을 하면
- $\frac{\partial z}{\partial x}=\frac{\partial z}{\cancel{\partial t}}\frac{\cancel{\partial t}}{\partial x}$처럼 서로 지울 수도 있다.
- 위 예시에서 연쇄법칙을 써서 미분 $\frac{\partial z}{\partial x}$를 구하면,
- $\frac{\partial z}{\partial t} = 2t$
- $\frac{\partial t}{\partial x} = 1$
- $\frac{\partial z}{\partial x}=\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}=2t\cdot 1=2(x+y)$
- 각 노드에서의 미분을 곱한다는 개념만은 꼭 기억해놓자.
5.2.3 연쇄법칙과 계산 그래프
-
위의 식을 계산 그래프로 나타내보자.
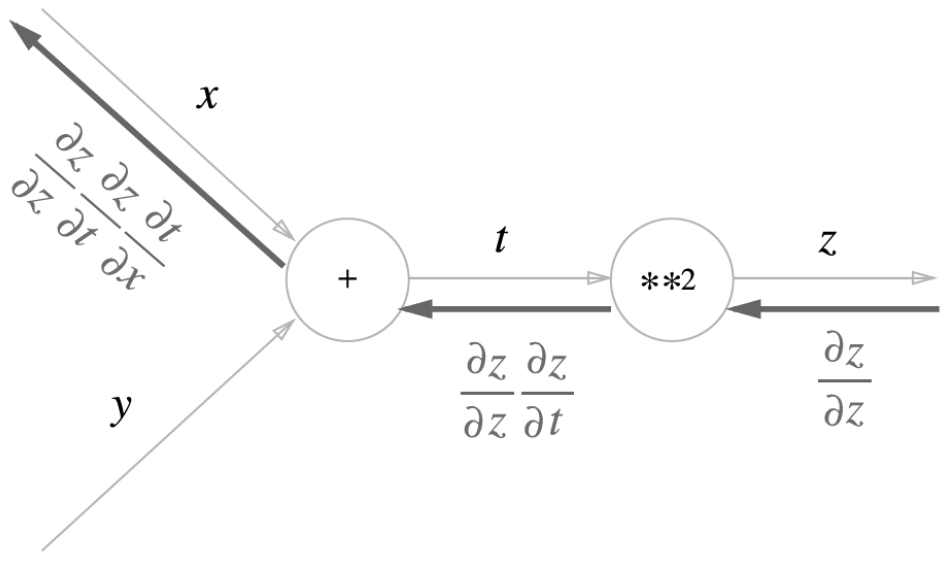
- 위에서 설명한 것과 같이, 역전파의 계선 절차에서는 오른쪽에서 왼쪽으로 절차를 진행한다.
- 들어온 입력 신호에 국소적 미분을 곱하여 다음 노드로 값을 전달한다.
- 위에서 설명한 것과 같이, 역전파의 계선 절차에서는 오른쪽에서 왼쪽으로 절차를 진행한다.
-
여기서 맨 왼쪽 값을 살펴보면,
- $\frac{\partial z}{\partial z}\frac{\partial z}{\partial t}\frac{\partial t}{\partial x} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial x} = \frac{\partial z}{\partial x}$가 성립되어 ‘$x$에 대한 $z$의 미분’이 된다.
- 즉, 역전파가 하는 일은 연쇄법칙의 원리와 같다.
5.3 역전파
- 위에선 계산 그래프의 역전파가 연쇄법칙에 따라 진행되는 것을 살펴봤다.
- $+$와 $\times$등의 연산을 예로 역전파의 구조를 살펴보자.
5.3.1 덧셈 노드 역전파
- $z=x+y$라는 식으로 역전파를 살펴보자.
- 해석적으로 미분을 계산해보면,
- $\frac{\partial z}{\partial x}=1, \frac{\partial z}{\partial y}=1$이다.
-
이를 계산 그래프로 보면 아래와 같다.
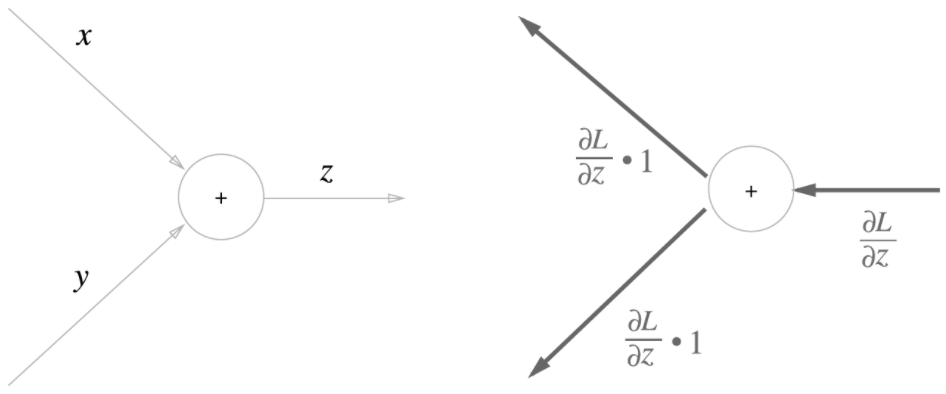
- 해석적으로 미분을 계산해보면,
- 즉, 덧셈 노드는 입력 신호를 다음 노드로 그대로 흘려보낸다.
5.3.2 곱셈 노드의 역전파
- $z=xy$식의 역전파를 살펴보자.
- $x$와 $y$에 대한 미분은
- $\frac{\partial z}{\partial x}=y, \frac{\partial z}{\partial y}=x$이다.
-
이를 계산 그래프로 그려보자.
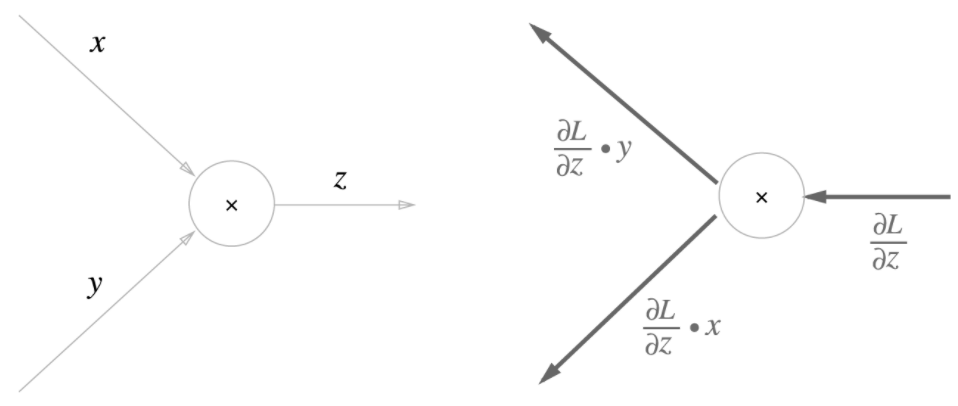
- $x$와 $y$에 대한 미분은
- 곱셈 노드는 서로 바꾼 값을 입력 신호와 곱해서 출력한다.
5.4 단순한 계층 구현하기
- 지금까지 본 사과 쇼핑의 예를 파이썬으로 구현해보자.
5.4.1 곱셈 계층
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
5.4.2 덧셈 계층
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
- 구현 자체는 간단하다.
5.5 활성화 함수 계층 구현하기
- ReLU와 Sigmoid 계층을 구현해보자.
5.5.1 ReLU계층
- ReLU함수의 수식을 복습해보자.
- $y=$
- $x (x>0)$
- $0 (x\leq0)$
- $y=$
- 위 식에서 $x$에 대한 $y$의 미분을 구하면,
- $\frac{\partial y}{\partial x}=$
- $1(x>0)$
- $0(x\leq0)$
- $x>0$이면 역전파는 상류의 값을 그대로 하류로 흘려보내고,
- $x\leq0$이면 신호를 보내지 않는다.(0을 보낸다.)
- $\frac{\partial y}{\partial x}=$
-
구현해보자.
class ReLU: def __init__(self): self.mask = None def forward(self, x): self.mask = (x <=0) out = x.copy() out[self.mask] = 0 return out def backward(self, dout): dout[self.mask] = 0 dx = dout return dxmask는 입력받은 numpy배열 중 0보다 작은 값의 위치를 저장하고, 이를 0으로 만들기 위한 장치로 사용되는 변수다.
5.5.2 Sigmoid 계층
- 시그모이드 함수를 복습해보자.
- $y=\frac{1}{1+\exp{(-x)}}$
- 0~1 범위의 S자 모양의 함수였다.
- $y=\frac{1}{1+\exp{(-x)}}$
-
위 식을 계산 그래프로 그리면 요렇게 그릴 수 있다.
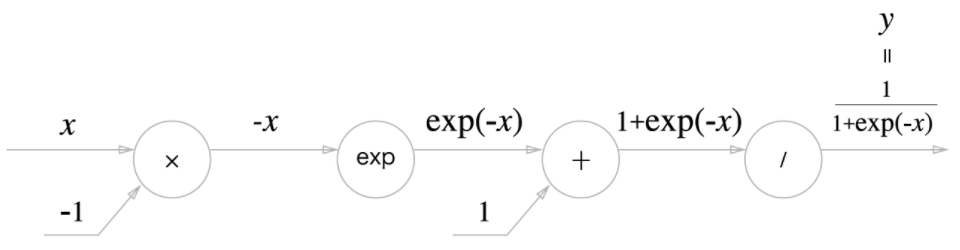
- 이전에 보지 못했던 $+, \times$노드 외에 $\exp, /$노드가 등장했다.
- 위 그래프의 흐름을 하나씩 살펴보자.
- $y=\frac{1}{x}$를 미분
- $\frac{\partial y}{\partial x} = \frac{1}{-x^1}=-y^2$
- 분수의 미분 참고
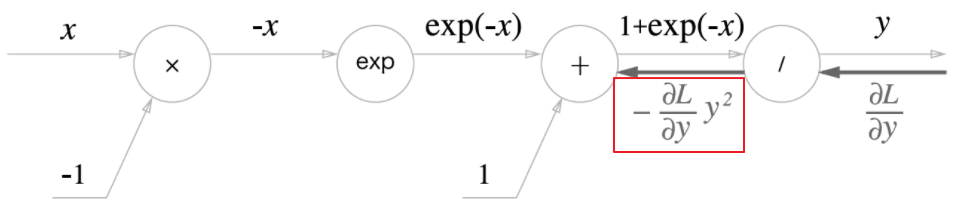
-
$+$노드는 단지 흘려보내는 작업만 수행한다.
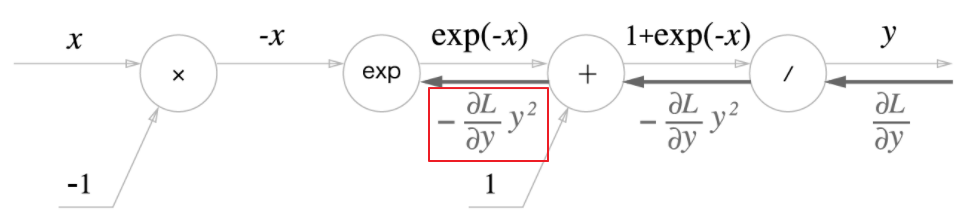
- $\exp$노드의 미분
- $\frac{\partial y}{\partial y} = \exp{(x)}$
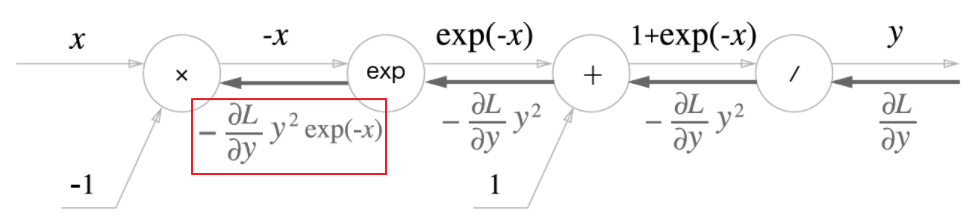
- 위 예에서는 $\exp{(-x)}$를 곱해 전파함
-
$\times$노드는 순전파 때의 값을 서로 바꿔 곱한다.
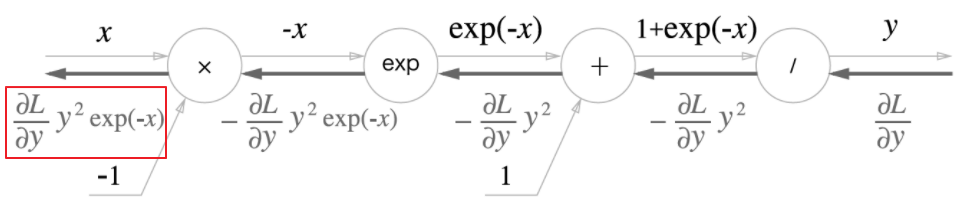
- $y=\frac{1}{x}$를 미분
- Sigmoid 계층의 역전파가 계산 그래프로 완료되었다.
- $\frac{\partial L}{\partial y}y^2\exp{(-x)}$
- 수식을 보면, $x, y$만으로 계산할 수 있다.
-
이를 축약하여…
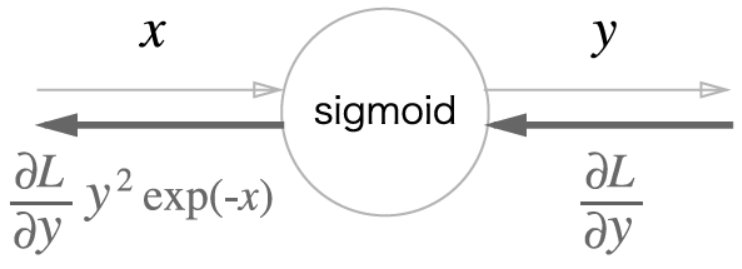
- 이렇게 Sigmoid 노드 하나로 대체할 수 있게 된다.
- 또한, $\frac{\partial L}{\partial y}y^2\exp{(-x)}$는 $y$에 대해 아래와 같이 정리할 수 있다.
-
$\frac{\partial L}{\partial y}y^2\exp{(-x)} = \frac{\partial L}{\partial y}\frac{1}{(1+\exp{(-x)})^2}\exp{(-x)}=\frac{\partial L}{\partial y}\frac{1}{1+\exp{(-x)}}\frac{\exp{(-x)}}{1+\exp{(-x)}}=\frac{\partial L}{\partial y}y(1-y)$
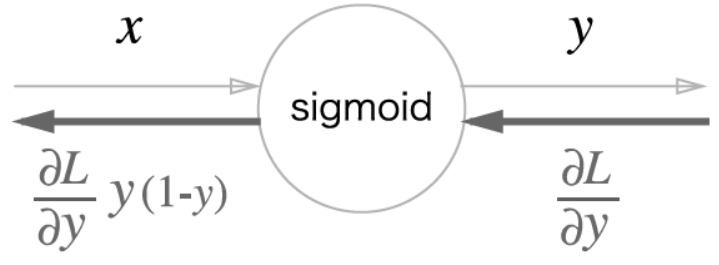
-
-
Sigmoid 계층을 파이썬으로 구현해보자.
class Sigmoid: def __init__(self): self.out = None def forward(self, x): out = 1 / (1+np.exp(-x)) self.out = out return out def backward(self, dout): dx = dout * (1.0-self.out) * self.out return dx
5.6 Affine/Softmax 계층 구현하기
5.6.1~2 Affine 계층(배치용까지)
- 순전파 시 수행하는 행렬의 곱을 기하학에선 어파인 변환(affine transformation) 이라고 함
- 이 책에선 어파인 변환을 수행하는 처리를 Affine 계층 이라는 이름으로 구현함
- 기본 선형대수 + 코드 위주의 내용이라서 내용 정리는 skip
5.6.3 Softmax-with-Loss 계층
- Softmax 복습
- Softmax 계층은 입력값을 정규화하여 출력한다. (총합이 1)
- 분류하고자 하는 클래스의 수만큼 출력한다. (숫자 손글씨의 경우 0~9, 10개)
- 이제 Softmax와 손실 함수인 교차 엔트로피 오차도 포함하여 Softmax-with-loss 계층을 살펴보자.
- (교차 엔트로피는 실제 레이블의 -log(Softmax 출력값) )
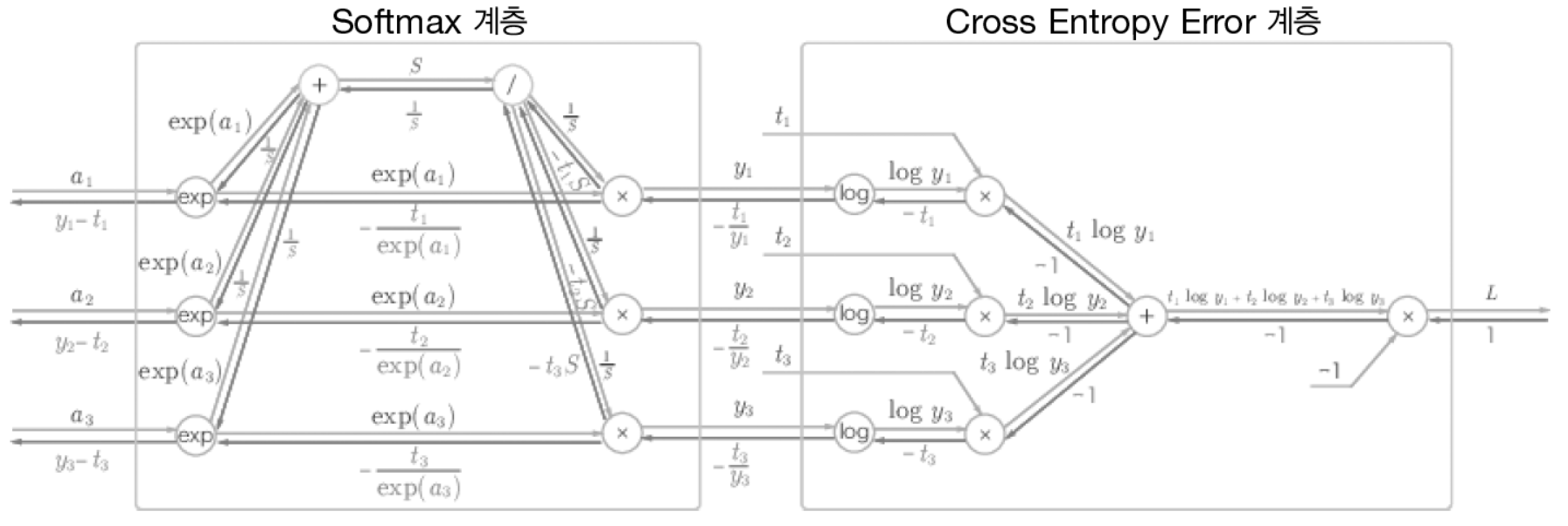
-
이를 간소화하면 아래와 같이 변환된다.
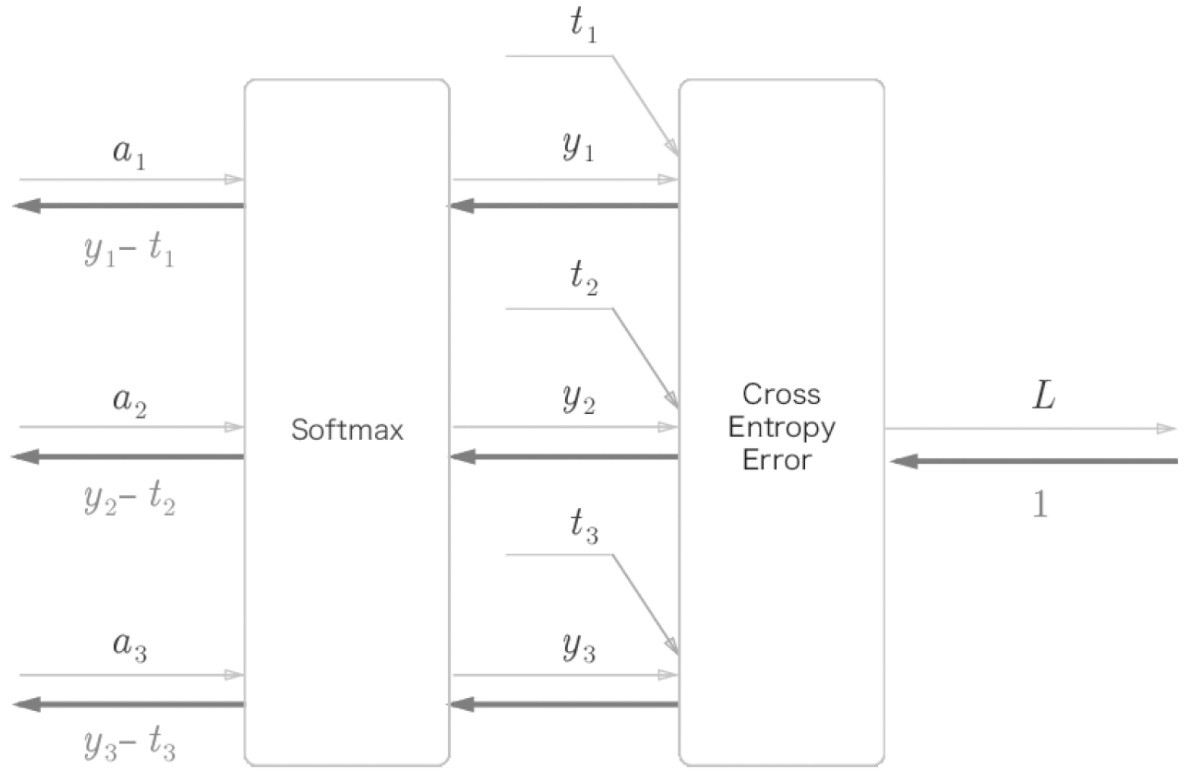
- 역전파 결과가 굉장히 간단한데, 소프트맥스의 출력값($y$)에서 정답 레이블($t$)와의 차이이다.
- 이는 교차 엔트로피 오차라는 함수가 원래 이렇게 설계되었기 때문이다.
- 회귀 출력층에서 항등 함수의 손실 함수로 오차제곱합을 사용하면 위와 결과와 같이 $(y-t)$값이 된다.
- 역전파 결과가 굉장히 간단한데, 소프트맥스의 출력값($y$)에서 정답 레이블($t$)와의 차이이다.
- 예를들어, 정답 레이블이 $(0, 1, 0)$ 이고, Softmax 출력이 $(0.3, 0.2, 0.5)$일 때,
- Softmax 역전파는 $(0.3, -0.8, 0.5)$라는 큰 오차를 전파한다.
-
이를 구현하면,
class SoftmaxWithLoss: def __init__(self): self.loss = None self.y = None self.t = None def forward(self, x, t): self.t = t self.y = softmax(x) self.loss = cross_entropy_error(self.y, self.t) return self.loss def backward(self, dout=1): batch_size = self.t.shape[0] dx = (self.y-self.t) / batch_size return dx- 역전파 때에는 전파하는 배치의 수로 나눠 데이터 1개당 오차를 아 계층으로 전파하는 점에 유의하자!
5.7 오차역전파법 구현하기
5.7.1 신경망 학습의 흐름 복습
신경망에는 적응 가능한 가중치, 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 ‘학습’이라 한다.
- 미니배치
- 훈련 데이터 중 일부를 무작위로 가져온다.
- 선별된 데이터를 미니배치라 하며, 이 미니배치의 손실 함수 값을 줄이는 것이 목표이다.
- 기울기 산출
- 미니배치 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구한다.
- 기울기는 손실 함수 값을 가장 작게 하는 방향을 제시한다.
- 여기서 앞에서 계속 배운 오차 역전파법이 등장한다.
- 원래는 기울기를 구하기 위해 수치 미분을 적용했지만, 시간이 오래 걸렸다.
- 오차역전파법을 이용하면 느린 수치 미분과 달리, 기울기를 효율적이고 빠르게 구할 수 있다.
- 매개변수 갱신
- 가중치 매개변수를 기울기 방향으로 아주 조금 갱신한다.
- 1~3을 반복한다.
요약
- 계산 그래프를 이용하면 계산 과정을 시각적으로 파악 가능
- 계산 그래프의 노드는 국소적 계산으로 구성되며, 국소적 계산을 조합해 전체 계산을 구성한다.
- 계산 그래프의 순전파는 왼쪽에서 오른쪽으로 계산을 수행한다.
- 역전파로는 각 노드의 미분을 구할 수 있다.
- 신경망의 구성 요소를 계층으로 구현하여 기울기를 효율적으로 계산할 수 있다. (오차역전파법)
- 수치 미분과 오차역전파법의 값을 비교하면, 오차역전파법의 구현에 에러가 없는지 확인할 수 있다. (기울기 확인)
댓글남기기