합성곱 신경망 CNN에 대해

7. 합성곱 신경망(CNN)

• CNN(convolutional neural network)은 이미지 인식, 음성 인식 등 다양한 곳에서 사용된다.
  • 특히 이미지 인식 분야에서 기초가 되는데, 매커니즘을 살펴보자.

7.1 전체 구조

• 신경망과 마찬가지로 CNN도 여러 계층을 조합하여 만들 수 있다.
  • 다만, 합성곱 계층(convolutional layer)과 풀링 계층(pooling layer)이 새롭게 등장한다.
• 앞선 장에서 살펴본 신경망은 인접하는 계층의 모든 뉴런과 결합되어있는데,
  • 이를 완전연결(fully-connected, 전결합)이라고 하며, 이는 Affine 계층으로 구현했다.

• CNN의 구조를 그림으로 살펴보자.

  

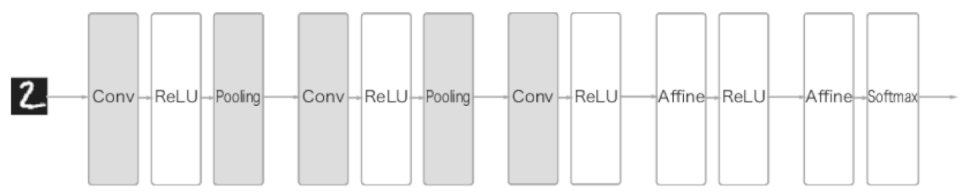
  • Conv-ReLU-(Pooling) 흐름으로 연결된다. (풀링 계층은 생략하기도 함)
  • 또한 출력에 가까운 층에서는 앞선 신경망과 같이 Affine-ReLU, Affine-Softmax 조합을 그대로 사용한다.

7.2 합성곱 계층

• CNN은 완전연결 신경망과 다르게 각 계층 사이에 3차원 데이터처럼 입체적인 데이터가 흐른다.

7.2.1 완전연결 계층의 문제점

• 완전연결 계층에서는 데이터의 형태를 무시한다.
  • 예를들어, 이미지 데이터는 3차원 형태인데, 완전연결 계층에서는 이를 한 줄로 세워버린다.
    • 그러면, 각 픽셀간 가지고있는 패턴, 특징 등이 모두 무시되어버린다.
    • RGB의 각 채널의 연관성이 무시되거나
    • 비슷한 위치에 있는 픽셀값은 비슷하다거나
    • 먼 픽셀끼리는 관련이 없거나 등…
• 반면, CNN에서는 데이터 형태를 보존한다.
  • 이미지도 3차원으로 그대로 받고, 다음 계층으로도 3차원으로 전달한다.
  • 그러면 이미지데이터를 더 잘 이해할 수 있는 가능성이 생긴다
  • CNN에서는 합성곱 계층의 입출력 데이터를 특징맵(feature map)이라고도 한다.
    • input feature map, output feature map…

7.2.2 합성곱 연산

• 합성곱 연산은 이미지 처리에서 필터 연산에 해당한다.
  • 필터를 커널이라고 칭하기도 한다.
• 필터의 윈도우를 일정 간격(스트라이드)으로 이동해가며 입력 데이터에 적용한다.
  • 윈도우에 해당되는 입력데이터 값과 필터를 곱하여 이 값들의 총합을 구한다.

  • 단일 곱셈-누산(fused multiply-add, FMA)라고 한다.

    

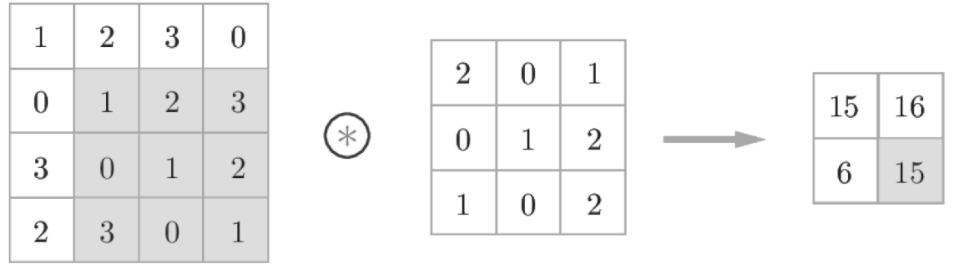
  • 위 예에서, 입력은 (4,4), 필터는 (3,3), 출력은 (2,2)가 된다.
• CNN에선 필터의 매개변수가 가중치에 해당하고,(완전연결에서의 기울기) 편향 또한 존재한다.

• 편향까지 포함한 계산 과정

  

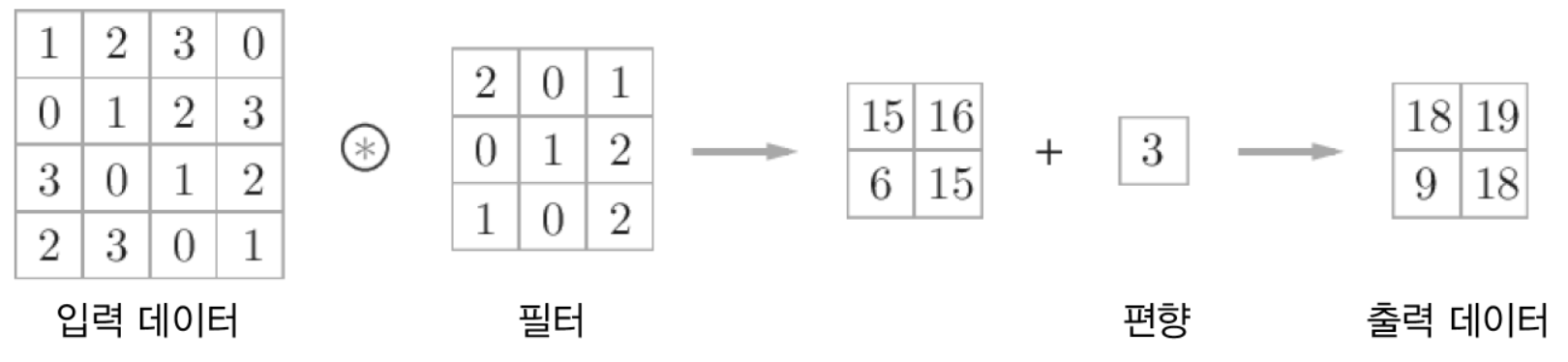
7.2.3 패딩

• 합성곱 연산을 하기 전, 입력 데이터의 테두리에 특정 값(0 등)을 채워넣는 것을 패딩이라고 한다.

  

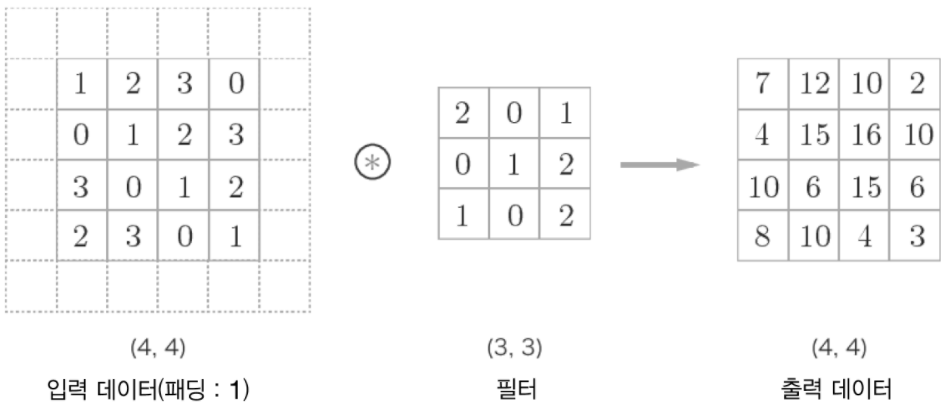
• 패딩을 하는 이유

  • 위에서 본 것처럼 입력 데이터와 필터와 합성곱 연산을 하면 출력 데이터의 형태가 축소된다.
  • 신경망이 깊어서 합성곱을 여러번 수행하다보면, 출력 데이터의 형태가 매우 작아지거나 1이 될 수 있다.
  • 이를 방지하기 위한 목적으로 사용한다.

7.2.4 스트라이드

• 필터를 적용하는 윈도우가 얼마나 움직이는지를 결정한다.
  • 스트라이드를 키우면 출력 크기는 작아지고, 스트라이드를 줄이면 출력 크기가 커진다.

  

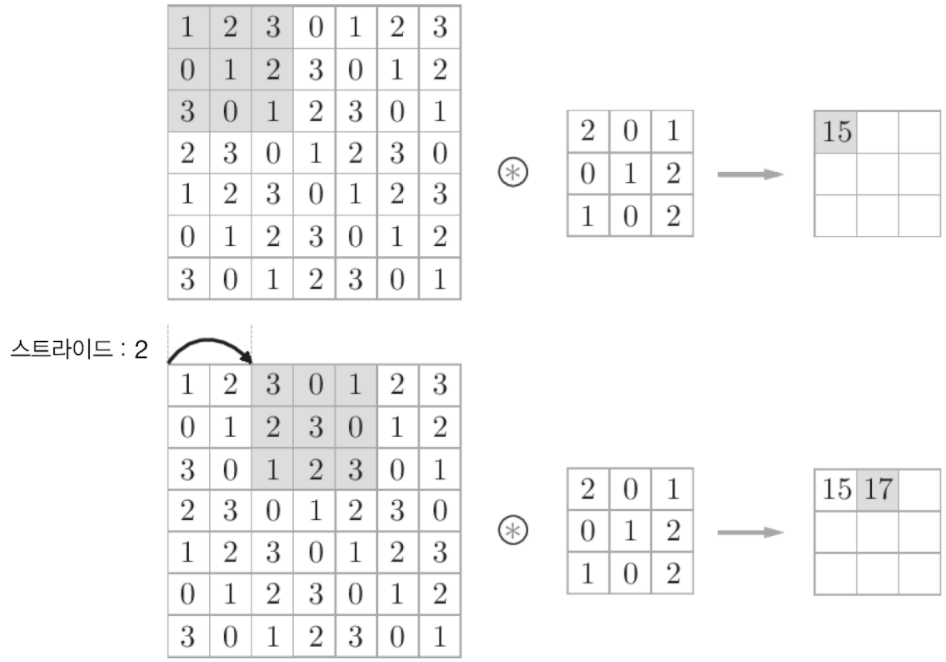
• 살펴본 것처럼 패딩과 스트라이드를 통해 출력 크기를 조절할 수 있다.
  • 그럼 패딩, 스트라이드와 입력 크기, 출력 크기 간의 관계를 수식화해보자.
  • 입력 크기: $(H, W)$, 필터 크기: $(FH, FW)$, 출력 크기: $(OH, OW)$, 패딩: $P$, 스트라이드: $S$
  • $OH = \frac{H+2P-FH}{S}+1$
  • $OW = \frac{W+2P-FW}{S}+1$
  • 프레임워크에 따라 이 값이 정수로 나누어 떨어지지 않더라도 이를 반올림하는 기능을 제공한다.

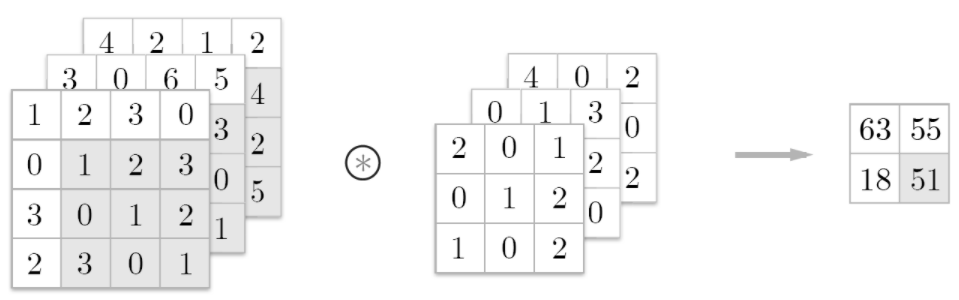
7.2.5 3차원 데이터의 합성곱 연산

• 지금까지는 2차원 데이터에서의 합성곱을 살펴봤지만, 3차원 데이터 합성곱 연산도 이와 유사하다. (3차원에서는 가로,세로에 채널 까지 고려)
  • 각 채널에 대응하는 필터가 있고, (대응하려면 입력데이터의 채널 수와 필터 채널수가 같아야함)

  • 채널간 합성곱한 결과를 더하여 출력함.

    

7.2.6 블록으로 생각하기

• 3차원 합성곱 연산을 직육면체 블록이라고 생각해보자.

  

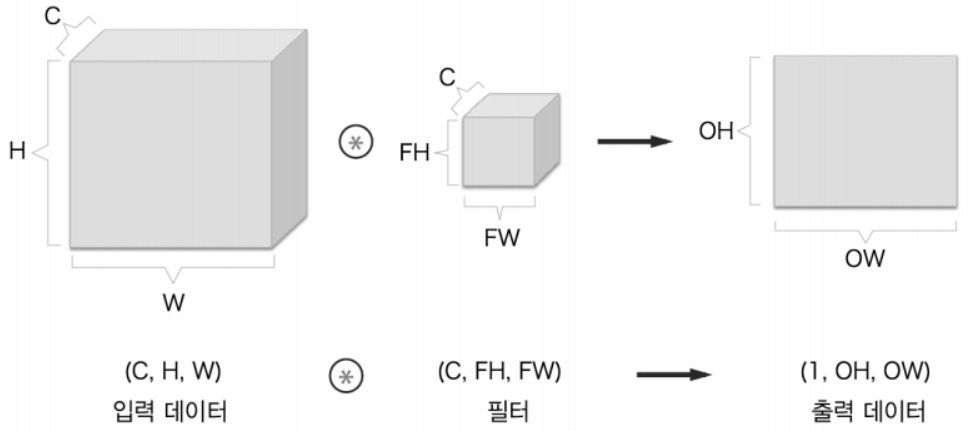
  • C개의 채널을 가진 입력 데이터와 필터를 합성곱하면, 1개의 채널을 가진 출력 데이터가 나온다.
  • 출력 데이터에서도 여러개의 채널을 가지게 하려면 어떻게 해야할까?

    • 필터를 여러개 사용하면 됨!

      

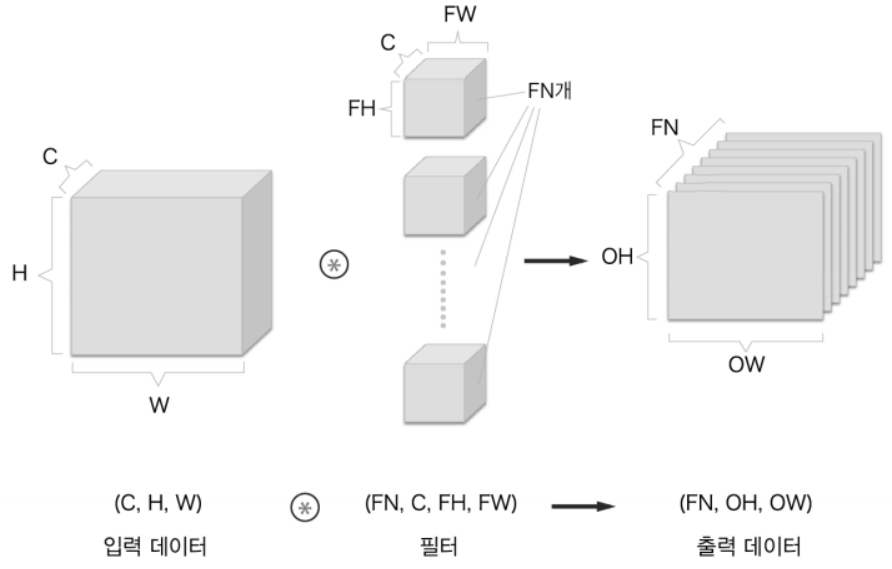
    • 즉, 필터의 수가 출력 데이터의 채널 수가 된다.

• 편향까지의 계산 과정을 그림으로 그리면 아래와 같다.

  

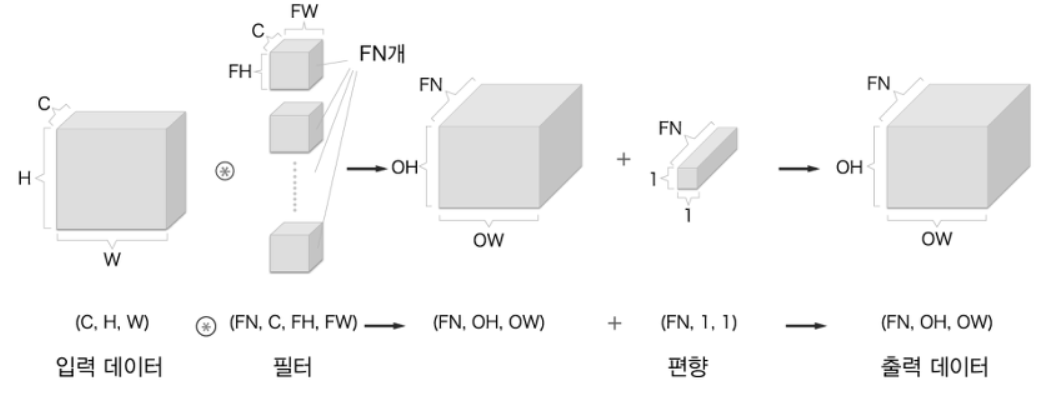
  • 편향 계산은 넘파이의 브로드캐스트 기능으로 쉽게 구현된다.

7.2.7 배치 관리

• 합성곱 연산에서도 계산의 효율을 위해 배치 처리를 지원한다.
  • 기존 (C, H, W)로 입력되던 데이터를, 데이터가 N개일 때 (N, C, H, W) 4차원으로 입력되어 각 계층을 타고 흐른다.
  • 신경망에 4차원 데이터가 하나 흐를 때, 데이터 N개에 대한 합성곱 연산이 이뤄진다.

7.3 풀링 계층

• 풀링은 공간을 줄이는 연산이다.

  

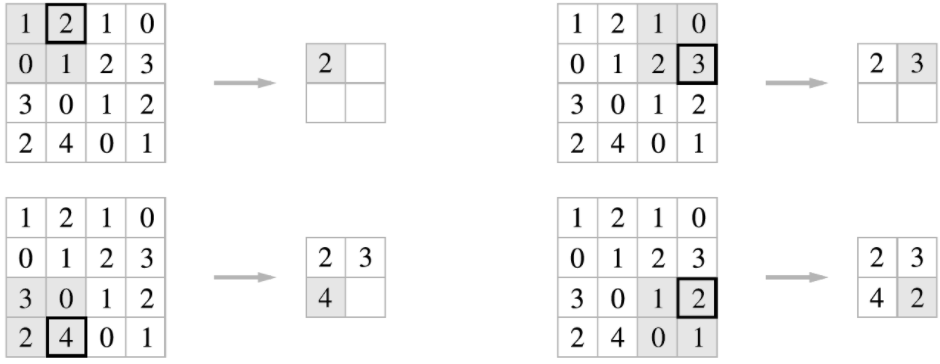
  • 위 예는 2x2 최대 풀링(max pooling)을 스트라이드 2로 처리하는 순서이다.
  • 2x2 영역이 스트라이드 단위로 움직이며(필터의 윈도우처럼) 가장 큰 값만(max) 꺼낸다.
  • 평균 풀링이라는 것도 있는데, 영역의 값들을 평균하여 꺼낸다.

7.3.1 풀링 계칭의 특징

• 학습할 매개변수가 없다.
  • 단지 최댓값을 찾거나 평균을 내는 등의 작업을 하기때문에, 매개변수가 필요없다.
• 채널 수가 변하지 않는다.
  • 채널마다 독립적으로 계산하기때문에 채널 수 그대로 출력데이터로 내보낸다.
  • 물론 이에 이 출력 데이터들을 모두 합한다던지 등의 연산을 하면 채널 수가 달라질 수는 있지만, 풀링 자체는 채널수에 영향을 끼치지 않는다.
• 입력의 변화에 영향을 적게 받는다.
  • 입력 데이터가 조금 변해도 풀링의 결과는 잘 변하지 않는다. (특히 최대 풀링일 경우)
  • 최대 풀링이면 데이터가 한 칸씩 밀린다고 하더라도 최댓값이 변하지 않음

7.4 CNN 시각화하기

• 지금까지 CNN이 어떻게 학습하는지를 알아봤지만,
• 실제로 모델이 어떻게 ‘보고’있는지는 잘 이해가 되지 않는다.
• 이번에는 모델이 입력 데이터를 어떻게 바라보고있는지 살펴보자.

7.4.1 1번째 층의 가중치 시각화하기

• 합성곱 계층 필터의 이미지를 살펴보자.

  

  • 학습 전에는 패턴이 없지만, 학습 후에는 어떤 패턴처럼 보이는 규칙들이 생성되었다.
  • 색이 바뀌는 필터(에지)와 덩어리진 영역(블롭) 등과 같은 정보를 추출해낸다.

• CNN에선 첫 층의 필터에서 추출한 정보를 뒷단 계층에 전달한다.

7.4.2 층 깊이에 따른 추출 정보 변화

• CNN 모델에선 첫 층에서는 에지, 블롭과 같이 단순한 정보만 파악한다.
• 층이 깊어질수록 추출되는 정보(강하게 반응하는 뉴런)는 더 추상화된다.
  • 예를들어 첫 층에서는 에지, 블롭
  • 4번째 층에서는 질감
  • 6번째 층에선 사물의 일부
  • 10번째 층에서는 사물의 카테고리
  • 와 같이 점차 의미를 이해해나가는 것처럼 학습해나간다.

  

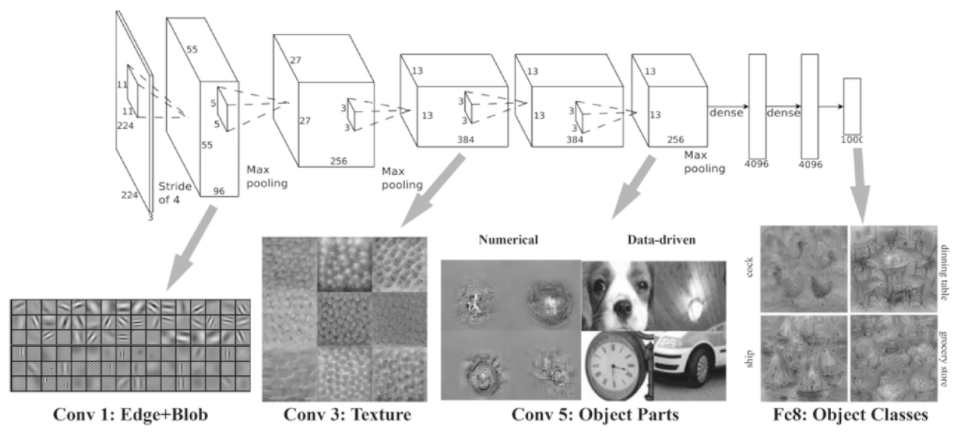
7.5 대표적인 CNN

• 다양한 네트워크가 있지만,
  • CNN의 원조격인 LeNet과
  • 딥러닝이 하이라이트받게 만든 AlexNet을 살펴보자.

7.5.1 LeNet

• LeNet은 손글씨 숫자를 인식하는 네트워크다.
• 합성곱 계층과 풀링 계층을 반복하고, 마지막엔 완전연결 계층을 거치며 결과를 출력한다.
• 최근의 방법과의 차이점을 알아보면,
  • LeNet은 활성화함수로 시그모이드를 사용한다. (요즘은 ReLU)
  • LeNet은 서브샘플링(풀링에서)을 하여 데이터를 줄인다. (최근엔 최대 풀링)

7.5.2 AlexNet

• LeNet과 마찬가지로 합성곱 계층과 풀링 계층을 거쳐 완전연결 계층을 통해 결과를 출력한다.
• LeNet과의 차이점은,
  • 활성화 함수로 ReLU를 사용한다.
  • LRN(Local Response Normalization)이라는 국소적 정규화를 실시하는 계층을 이용한다.
  • 드롭아웃을 사용한다.

---

요약

• CNN은 완전연결 계층 네트워크에 합성곱 계층과 풀링 계층을 추가한다.
• CNN을 시각화해보면, 계층이 깊어질수록 의미가 있는 정보를 추출하는 모습을 보인다.
• 대표적인 네트워크는 LeNet, AlexNet이 있다.
• 딥러닝 발전에는 빅데이터와 GPU가 크게 기여했다.