신경망에 대해 알아보자
업데이트:
3. 신경망
퍼셉트론은 이론상 복잡한 처리도 표현할 수 있지만, 가중치를 여전히 수동으로 설정해야한다.
신경망은 데이터를 통해 가중치를 자동으로 학습하는데, 이 신경망의 개요를 살펴보자.
3.1 퍼셉트론에서 신경망으로
- 퍼셉트론과 신경망은 공통점이 많다.
- 퍼셉트론과 신경망이 어떻게 다른지에 대해 알아보자.
3.1.1 신경망의 예
- 신경망은 입력층, 은닉층, 출력층으로 구성되어있다.
- 여기서 은닉층은 사람 눈에는 보이지 않는다.
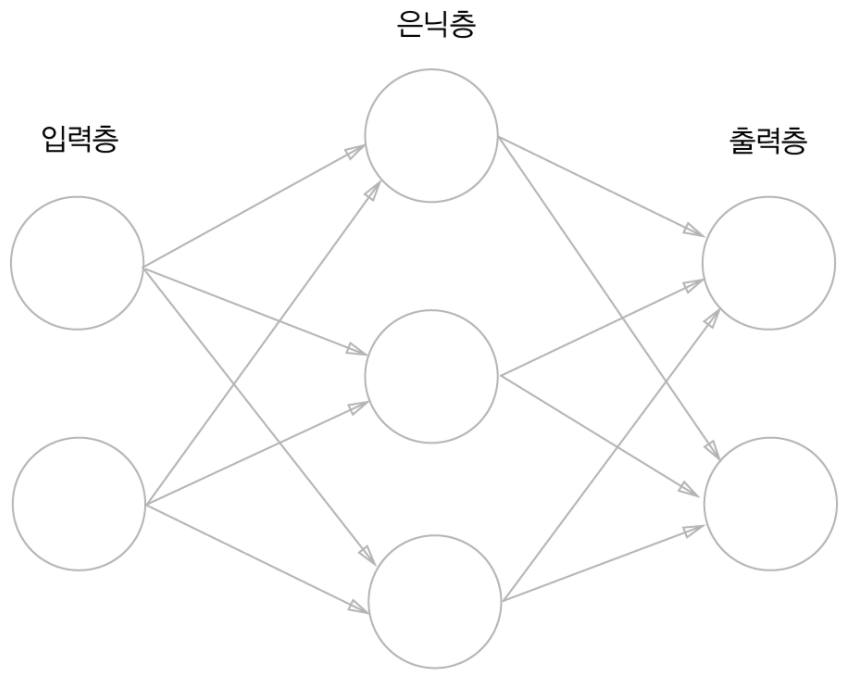
- 근데 위 구조를 살펴보면 퍼셉트론과 크게 달라보이지 않는다.
- 그럼, 신경망에서는 신호를 어떻게 전달할까?
3.1.2 퍼셉트론 복습
-
아래 그림은 $x_1$과 $x_2$ 두 신호를 입력받아 $y$를 출력하는 퍼셉트론이다.
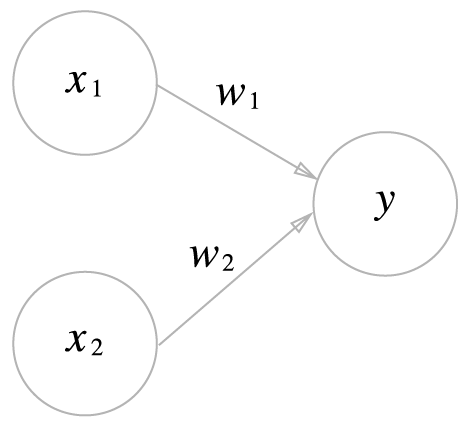
- 수식은,
- $y=$
- $0\,(b+w_1x_1+w_2x_2\leq0)$
- $1\,(b+w_1x_1+w_2x_2>0)$
- 이다. (mathjax에서 begin-end 수식이 안 먹어서 일단 위처럼 표시함…)
- $y=$
- 여기서 $b$는 편향을 나타내는 매개변수인데, 위 그림에서는 보이지 않는다.
-
편향까지 포함하여 나타내보자.
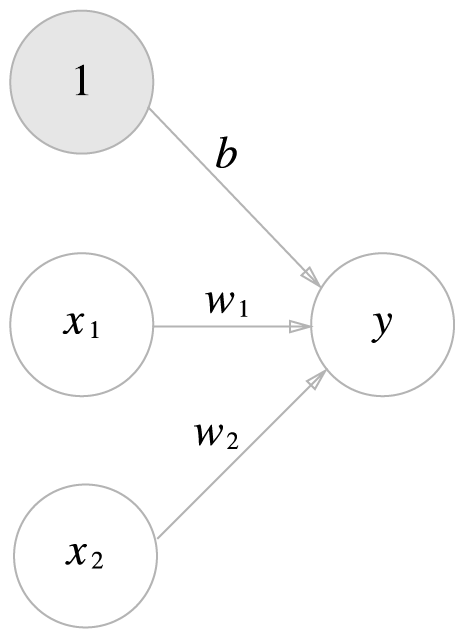
- 가중치가 $b$이고, 입력이 1인 뉴런이 추가됨으로써 편향을 나타냈다.
- 편향의 입력신호는 항상 1이므로 회색으로 구별
- 위 그림을 보다 간결하게 수식으로 나타내보자.
- $y=h(b+w_1x_1+w_2x_2)$
- $h(x)=$
- $0\,(x\leq0)$
- $1\,(x>0)$
- 위 식은 입력 신호의 총합이 $h(x)$라는 함수를 거쳐 변환되어, 그 값이 y의 출력이 된다.
- $h(x)$함수는 입력이 0을 넘으면 1을 돌려주고, 아니면 0을 반환한다.
- 가중치가 $b$이고, 입력이 1인 뉴런이 추가됨으로써 편향을 나타냈다.
3.1.3 활성화 함수
- 위 식의 $h(x)$와 같이, 입력 신호의 총합을 출력 신호로 변환하는 함수를 일반적으로 활성화 함수(avtivation function)라 한다.
- 활성화라는 말에서 느껴지듯, 입력 신호의 총합이 활성화를 일으키는지 정하는 역할!
- 활성화 함수를 포함하여 처리 과정을 시각적으로 살펴보자.
- 일단 수식부터
- $a=b+w_1x_1+w_2x_2$
- $y=h(a)$
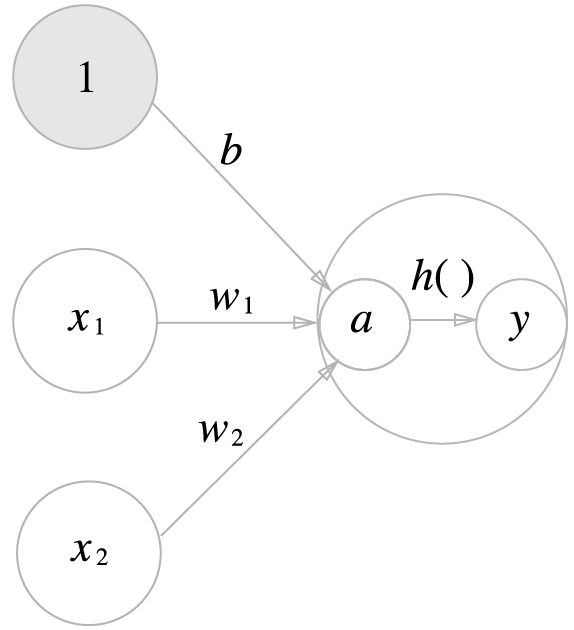
- 편향을 포함한 가중치 신호의 합계가 $a$가 되고,
- 활성화 함수 $h()$를 거쳐 $y$라는 노드로 변환된다.
- 노드 = 뉴런
- 일단 수식부터
3.2 활성화 함수
- 위 식에서의 활성화 함수$h()$는 임계값을 경계로 출력이 바뀌는데, 이를 계단 함수라고 한다.(step function)
- 그래서 퍼셉트론에서는 활성화 함수로 계단 함수를 사용한다 고 할 수 있다.
- 그 외 활성화 함수들에 대해 살펴보자. 궁금궁금.
3.2.1 시그모이드 함수
- 신경망에서 자주 이용하는 활성화 함수인 시그모이드 함수의 식은 아래와 같다.
(모두의 딥러닝 - 로지스틱 회귀 파트 공부할 때 갑자기 나와서 당황했던 기억)-
$h(x) = \frac{1}{1+exp(-x)}$
- $exp(-x)$는 $e^{-x}$를 뜻하며, $e$는 자연 상수 $2.7182…$의 값을 갖는 실수이다.
-
- 신경망에서는 활성화 함수로 시그모이드를 이용하여 신호를 변환하고, 그 신호를 다음 뉴런에 전달한다.
- 그 외 다층의 구조와 신호를 전달하는 방식은 기본적으로 퍼셉트론과 같다.
3.2.2 계단 함수 구현하기
-
계단함수를 구현해보자.
def step_function(x): return 1 if x > 0 else 0- 다만 이렇게 구현하면, x의 형태가 int, float 등일때만 가능하고, 배열일 때에는 불가능하다.
-
배열일 때에도 지원이 되도록 구현해보자.
def step_function(x): y = x>0 return y.astype(np.int)- numpy의 기능을 이용하여 bool 자료형으로 만들어내고, 이것을 다시 int로 변환한다.
3.2.3 계단 함수의 그래프
-
계단 함수의 그래프를 그려보자.
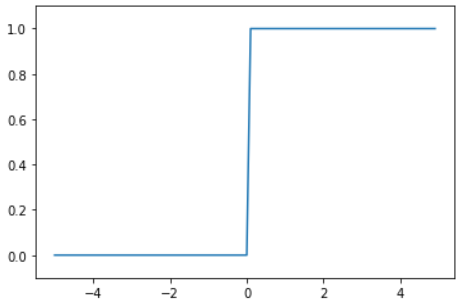
- 모양이 0을 기준으로 계단 모양으로 생겼다! 이름에 충실한 함수.
3.2.4 시그모이드 함수 구현하기
-
시그모이드 함수를 구현해보자.
def sigmoid(x): return 1 / (1 + np.exp(-x))- 요렇게 구현하면, 넘파이 배열을 넣어도 잘 처리되는데, 넘파이의 브로드캐스트 기능덕분에 가능.
-
시그모이드 함수 그래프를 그려보자.
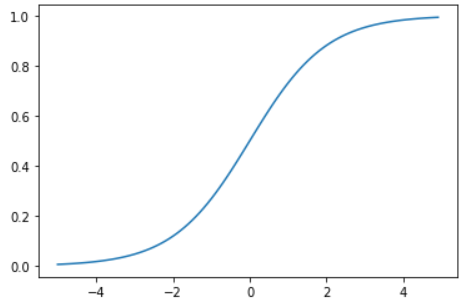
- 계단함수는 이름에 충실한데, 시그모이드는 와닿지가 않았다.
- 근데, 시그모이드(sigmoid)라는 말이 ‘S자 모양’ 이라는 뜻이라고 한다! 납득 가능!
- 계단함수는 이름에 충실한데, 시그모이드는 와닿지가 않았다.
3.2.5 시그모이드 함수와 계단 함수 비교
-
두 함수를 그래프로 비교해보자.
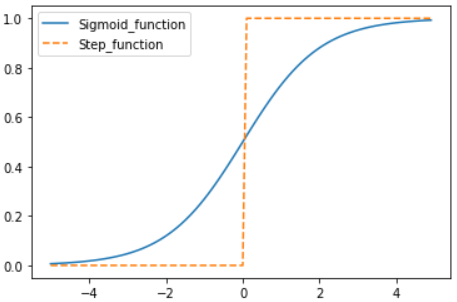
- 공통점
- 두 함수 모두 입력값이 작으면 0, 크면 1에 가까워지는(혹은 되는) 출력을 보여준다.
- 또한, 출력의 범위가 0과 1 사이이다.
- 비선형 함수다.
- 차이점
- 계단 함수는 임계값 0을 기준으로 출력이 0과 1로 급격히 변하는데,
- 시그모이드 함수는 연속성을 갖고있다.
- 시그모이드 함수의 ‘매끄러움’이 신경망 학습에선 중요한 역할을 한다.
3.2.6 비선형 함수
- 신경망에서는 활성화 함수로 비선형 함수를 사용해야한다.
- 그 이유로는, 선형 함수를 이용하면, 신경망의 층을 깊게 하는 의미가 사라지기 때문이다.
- 이유를 간단히 살펴보면,
- $h(x) = cx$라는 활성화 함수로 3층 네트워크를 만들어보자.
- 그러면, $y(x) = h(h(h(x)))$가 될 것인데,
- 이것은 결국 $y(x) = c * c * c * x$와 같고,
- 다시 표현하면 $y(x) = c^3x$이며,
- $c^3$은 여전히 상수이기때문에,
- 결국 $y(x) = ax$의 형태를 띈다. ($a = c^3$)
- 그래서, 여러 층을 쌓음으로써 이익을 보려면 비선형 함수를 이용해야한다.
3.2.7 ReLU 함수
- 시그모이드 함수는 오래전부터 이용했으나, 최근에는 ReLU(Rectified Linear Unit) 함수를 주로 이용한다.
-
ReLU는 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력한다.
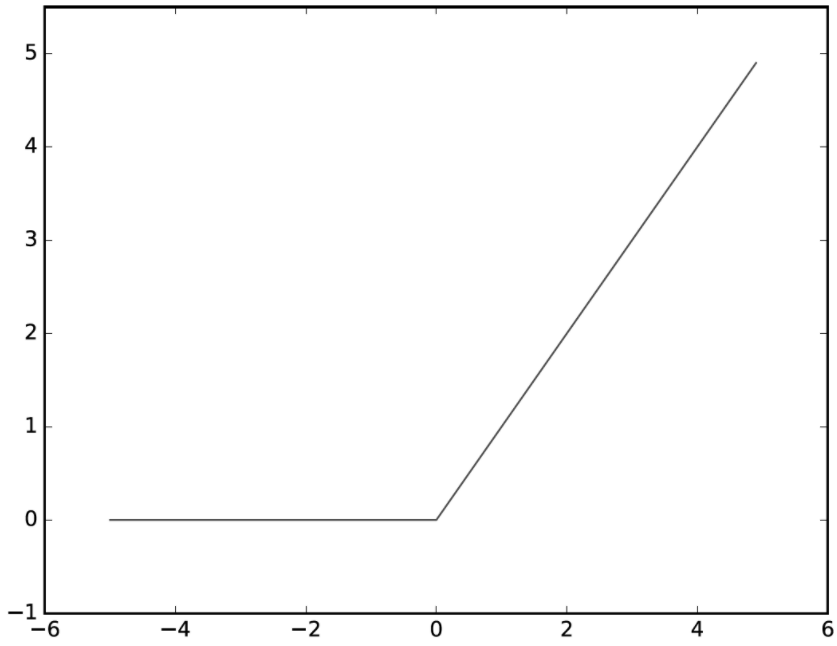
- ReLU의 수식
- $h(x)=$
- $x\,(x>0)$
- $0\,(x\leq0)$
- $h(x)=$
-
ReLU의 구현
def ReLU(x): return np.maximum(x, 0)
- ReLU의 수식
3.3 다차원 배열의 계산
- 넘파이의 곱을 이용하면 신경망 구현을 쉽게 할 수 있다.
X = np.array([1, 2])
W = np.array([[1, 3, 5], [2, 4, 6]])
Y = np.dot(X, W)
print(Y) # [ 5 11 17]
3.4 3층 신경망 구현하기
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identify_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [0.31682708 0.69627909]
3.5 출력층 설계하기
- 신경망은 분류, 회귀 모두에 이용 가능하다.
- 어떤 문제냐에 따라 출력층에서 사용하는 활성화 함수가 달라지는데,
- 일반적으로는 회귀에선 항등 함수
- 분류에서는 소프트맥스 함수를 사용한다.
3.5.1 항등 함수와 소프트맥스 함수 구현하기
- 항등함수
-
입력을 그대로 출력
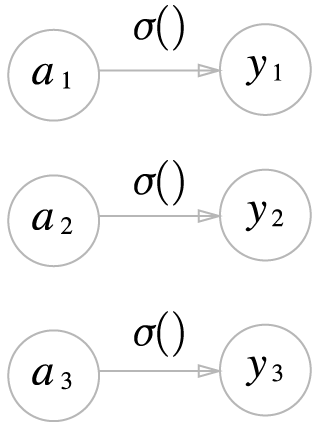
-
- 소프트맥스 함수(softmax function)
-
$y_k = \frac{\exp{(a_k)}}{\sum^n_{i=1}{\exp{(a_i)}}}$
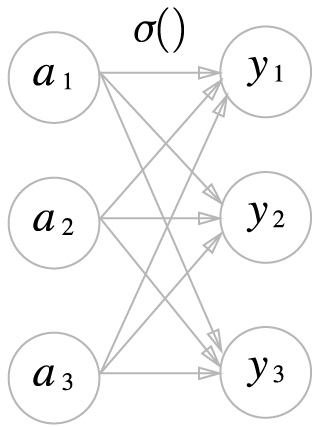
- 수식에서 알 수 있듯, 모든 입력을 받아 지수 함수의 합을 구하기 때문에, 출력값이 모든 화살표를 받게 된다.
-
코드로 구현하면 아래와 같다.
def softmax(x): exp_a = np.exp(a) sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y
-
3.5.2 소프트맥스 함수 구현 시 주의점
- 위에서 구현한 함수는 컴퓨터로 계산 시, overflow 문제가 발생한다.
- 지수함수의 계산값이 매우, 혹은 무한히 커지기 때문에 이 값들을 다시 나누면 불안정해진다.
-
$y_k =\frac{\exp{(a_k)}}{\sum^n_{i=1}\exp{a_i}}= \frac{C\exp(a_k)}{C\sum^n_{i=1}\exp{(a_i)}} =\frac{\exp(a_k+\log{C})}{\sum^n_{i=1}\exp{(a_i+\log{C})}}=\frac{\exp(a_k+C^,)}{\sum^n_{i=1}\exp{(a_i+C^,)}}$
- 위 수식을 통해, 오버플로 문제를 개선할 수 있다.
- 일반적으로는 $C^,$에 입력 신호 중 최댓값을 이용하여 오버플로를 막는다.
-
이것을 반영하여 다시 코드로 구현하면 아래와 같다.
def softmax(a): c = np.max(a) exp_a = np.exp(a-c) # 오버플로 방지 sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y
3.5.3 소프트맥스 함수의 특징
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y) # [0.01821127 0.24519181 0.73659691]
print(np.sum(y)) # 1.0
- 소프트맥스 함수의 출력은 0부터 1.0 사이이며,
- 소프트맥스 함수 출력의 총합은 1이다.
- 이것이 매우 중요한 특징인데,
- 이 성질 덕분에 소프트맥스 함수의 출력을 ‘확률’로 해석할 수 있다.
- 예를들어, 소프트맥스 함수의 출력이 [0.018, 0.245, 0.737] 이라면,
- y[0]의 확률은 1.8%, y[1]의 확률은 24.5%, y[2]의 확률은 73.7%라고 해석이 가능하다.
- 혹은 가장 높은 확률로 계산해서, 답은 y[2]이다. 라고 해석할 수도 있다.
- 예를들어, 소프트맥스 함수의 출력이 [0.018, 0.245, 0.737] 이라면,
- 주의할 점은, 소프트맥스 함수를 적용해도 각 원소의 대소관계는 변하지 않는다.
- 지수 함수는 단조 증가 함수이기 때문.
- (단조 증가 함수: $a \leq b$일 때, $f(a) \leq f(b)$)
- 신경망을 이용한 분류에서는, 일반적으로 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식함.
- 지수 함수를 씌우나 안 씌우나(소프트맥스 함수를 쓰나 안 쓰나) 어차피 큰 값으로 출력을 하기 때문에,
- 지수 함수 계산에 드는 자원 낭비를 줄이고자 출력층의 소프트맥스 함수는 생략하는 것이 일반적. (함수를 적용하나, 안 적용하나 결과가 똑같으니까!)
- 지수 함수를 씌우나 안 씌우나(소프트맥스 함수를 쓰나 안 쓰나) 어차피 큰 값으로 출력을 하기 때문에,
3.5.4 출력층의 뉴런 수 정하기
- 해결하려는 문제에 맞게 적절히 정해야 함.
- 예를들어, 분류 문제라면, 분류하고 싶은 클래스의 수로 설정.
3.6 배치 처리
-
MNIST 사진 한 장을 입력했을때의 배열을 생각해보자.

- 784개의 원소로 구성된 1차열 배열이 입력되어, 나중엔 원소가 10개인 1차열 배열로 출력된다.
-
그럼 이미지를 여러 장을 한꺼번에 입력하면 어떻게 될까요?

- 입력 데이터는 100 * 784, 출력 데이터는 100 * 10 형태로 된다.
- 100장 분량 입력 데이터의 결과가 한 번에 출력되는 것을 나타내는데,
- 이렇게 하나로 묶은 입력 데이터를 배치(batch)라고 한다.
- 왜 배치로 입력해야할까?
- 수치 계산 라이브러리 대부분이 큰 배열을 효율적으로 처리할 수 있도록 설계됨
- 데이터 전송이 병목으로 작용하는 경우가 잦은데, 배치 처리를 통해 부하를 줄임
- 배치 처리는 큰 배열로 이뤄진 계산을 하게 되는데, 컴퓨터는 큰 배열을 한꺼번에 계산하는것이 작은 배열을 여러번 처리하는것보다 빠르다.
- 결국엔 컴퓨터와 라이브러리 특성상 큰 데이터를 한 번에 처리하는것이 효율적이기 때문!
-
구현하면 아래와 같다.
x, t = get_data() network = init_network() batch_size = 100 accuracy_cnt = 0 for i in range(0, len(x), batch_size): x_batch = x[i:i+batch_size] y_batch = predict(network, x_batch) p = np.argmax(y_batch, axis=1) accuracy_cnt += np.sum(p == t[i:i+batch_size]) print('Accuracy:'+str(float(accuracy_cnt)/len(x)))
요약
- 신경망은 활성화 함수로 시그모이드 함수, ReLU함수 같은 매끄럽게 변하는 함수를 이용한다.
- 출력층의 활성화 함수로는 일반적으로
- 회귀: 항등 함수
- 분류: 소프트맥스 함수 를 이용한다.
- 분류에서는 출력층의 뉴런 수를 분류하려는 클래스 수와 같게 설정한다.
- 입력 데이터를 여러개로 묶은 것을 배치라 하며, 배치를 통해 더 빠르게 계산할 수 있다.
댓글남기기