신경망은 어떻게 학습할까? (ft. 미분)

업데이트: October 02, 2020

4. 신경망 학습

학습?
- 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 찾는 것.
신경망이 학습할 수 있도록 해주는 지표인 손실 함수를 살펴보자.
- 손실 함수의 결괏값을 가장 작게 만드는 가중치 매개변수를 찾는 것이 학습의 목표

4.1 데이터에서 학습한다!

신경망의 가장 큰 특징은 데이터를 보고 학습을 할 수 있다는 점이다.
- 만약 이를 수동으로 한다면, 많게는 수천, 수만개의 매개변수에 대해 하나씩 매개변수를 입력해줘야한다.
참고로, 퍼셉트론도 직선으로 분리할 수 있는 문제라면, 데이터로부터 자동으로 학습이 가능하다.
- 퍼셉트론 수렴 정리로 증명되었으며, 다만 비선형 문제는 자동으로 학습이 불가능하다.

4.1.1 데이터 주도 학습

패턴을 찾는 등의 문제를 해결할 때, 주로 사람이 이런 저런 것들을 생각해서 답을 찾는 경우가 많다.
- 예를들어, 손글씨 분류를 할 때 숫자들의 특징은 이러니까 이 숫자는 2다!
기계학습에서는 이런 사람의 개입을 최소화하고, 데이터를 통해서 패턴을 찾고자 한다.
예를들어, 숫자 5를 제대로 분류하는 문제를 푼다고 생각해보자.
1. 사람이 직접 밑바닥부터 알고리즘을 설계한다면,
  - 숫자 5는 습관에 따라 모양이 다양하기때문에 쉽지 않다.
2. 데이터를 활용하여, 이미지에서 특징을 추출하고 그 특징의 패턴을 기계학습으로 학습시킨다.
  - 특징이란: 입력 데이터에서 본질적인 데이터를 추출할 수 있도록 설계된 변환기
    - 이미지에선 벡터, 컴퓨터 비전에서는 SIFT, SURF, HOG 등
  - 1) 보다는 효율이 높겠지만, 여전히 특징을 추출할 때 사람의 개입이 들어간다.
    - 즉, 적절한 특징을 사람이 찾지 못하면 좋은 결과를 얻지 못할 수 있다.
3. 신경망(딥러닝) 방식은 데이터(이미지)를 있는 그대로 입력시켜 스스로 학습한다.
  - 신경망은 이미지에 포함된 중요한 특징까지 스스로 학습힌다.
이를 보다 알기 쉽게 이미지로 나타내보자.
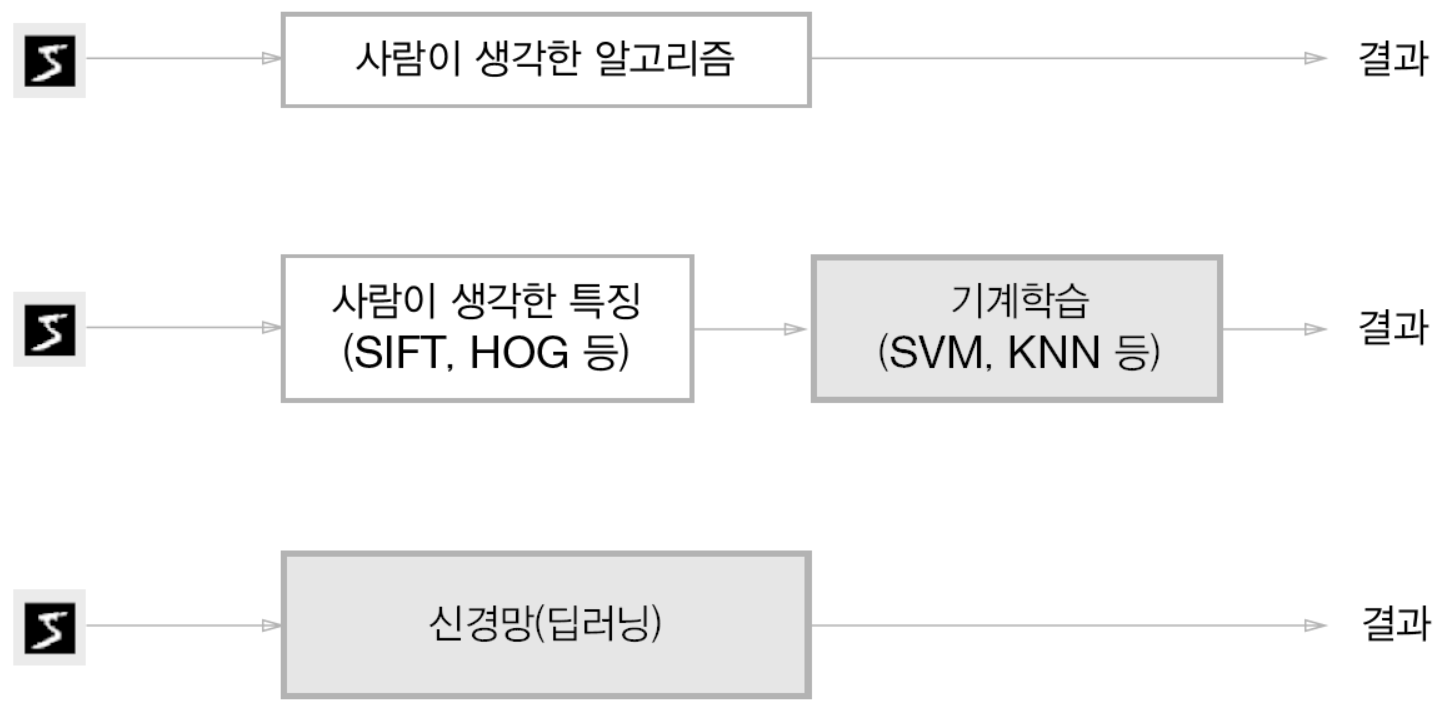
- 즉, 신경망은 모든 문제를 주어딘 데이터를 그대로 입력 데이터로 활용해 ‘end-to-end’로 학습할 수 있다.

4.1.2 훈련 데이터와 시험 데이터

오버피팅을 피하기 위해 훈련데이터로 훈련 후, 시험 데이터로 범용성을 테스트한다.
범용성이 떨어진다면, 새로운 문제(새로운 레코드)에 대해 제대로 작동하지 않을 수 있다.

4.2 손실 함수

신경망 학습에서는 현재의 상태를 ‘하나의 지표’로 표현한다.
- 이 지표를 가장 좋게 만들어주는 가중치 매개변수를 탐색한다.
신경망 학습에서 사용하는 지표는 손실 함수(loss function)라고 한다.
- 일반적으로는 오차제곱합과 교차 엔트로피 오차를 사용한다.

4.2.1 오차제곱합

가장 많이 쓰이는 손실 함수는 오차제곱합이며, 수식을 살펴보자.
- $E = \frac{1}{2}\sum_k{(y_k-t_k)^2}$
  - $y_k$: 신경망의 출력(예측값)
  - $t_k$: 실제값

0~9 손글씨 숫자 인식에서의 오차제곱합을 구해보자.

소프트맥스 함수로 출력한 예측값의 오차제곱합을 구해보자. (예측:2, 실제:2)

  def sum_squares_error(y, t):
      return 0.5 * np.sum((y-t)**2)

  y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
  t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
  np.argmax(y)    # 2
  sum_squares_error(np.array(y), np.array(t))    # 0.09750000000000003

그럼, 이번에는 예측:7, 실제:2 일 경우를 구해보자.

  y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
  t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
  np.argmax(y)    # 7
  sum_squares_error(np.array(y), np.array(t))    # 0.5975

오차제곱합의 기준으로는 첫 번째 추정 결과가 정답에 가까울 것으로 판단할 수 있다.

4.2.2 교차 엔트로피 오차

교차 엔트로피 오차(cross entropy error, CEE)도 자주 이용하는데, 수식을 살펴보자.
- $E=-\sum_k{t_k\log{y_k}}$
  - $t_k\log{y_k}$는 사실상 정답 레이블에 해당하는 예측값의 자연로그를 계산하는 식.
  - 예를들어, 정답 레이블이 ‘2’이고, 이 때 신경망 출력이 0.6이라면,
    - $-\log{0.6}=0.51$
코드로 구현해보자.
```
  def cross_entropy_error(y, t):
      delta = 1e-7
      return -np.sum(t*np.log(y+delta))
```
- 수식에 log 내에 delta가 더해지는데, 이 델타는 매우 작은 값이다.
- $\log0$이 되는 현상을 피하기 위해 더해준다.

예측:2, 실제:2 일 때의 교차 엔트로피 오차

  y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
  t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
  cross_entropy_error(np.array(y), np.array(t))    # 0.510825457099338

예측:7, 실제:2 일 때의 교차 엔트로피 오차

  y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
  t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
  cross_entropy_error(np.array(y), np.array(t))    # 2.302584092994546

정답일 때의 출력의 오차가 더 작게 나오는 것을 확인할 수 있다.

4.2.3 미니매치 학습

지금까지는 데이터 하나에 대한 손실 함수만 생각했다.
- 이제는 훈련 데이터 모두에 대한 손힐 함수의 합을 구하는 방법을 생각해보자.
교차 엔트로피 오차는 아래과 같이 구할 수 있다.
- $E=-\frac{1}{N}\sum_n\sum_k{t_{nk}}{\log{y_{nk}}}$
  - 데이터가 $N$개라면 $t_{nk}$는 $n$번째 데이터의 $k$번째 값을 의미한다.
  - 그리고 마지막에 데이터의 수 $N$으로 나누어 ‘평균 손실 함수’를 구한다.
그런데, 데이터가 많아진다면 손실 함수의 합을 구하는데 시간이 걸린다.
- 이를 위해 데이터의 일부를 추려 전체의 ‘근사치’로 이용할 수 있다.
- 신경망 학습에서도 훈련 데이터로부터 일부만 골라 학습을 하는데,
이 일부를 미니배치(mini-batch)라고 한다.
- 예를들어, 6만개의 훈련 데이터 중, 100개를 무작위로 뽑아 학습하는 것이다.
  - 이런 것을 미니배치 학습이라고 한다.
numpy로 구현 시, np.random.choice(train_size, batch_size) 로 미니배치들을 뽑아내 계산한다.

4.2.4 (배치용) 교차 엔트로피 오차 구현하기

위에서 구현한 교차 엔트로피 오차를 일부 수정하면 가능하다.

데이터가 하나인 경우와 데이터가 배치로 묶여 입력될 경우를 모두 고려하여 구현해보자.

  def cross_entropy_error(y, t):
      if y.ndim == 1:
          t = t.reshape(1, t.size)
          y = y.reshape(1, y.size)
      batch_size = y.shape[0]
      return -np.sum(t * np.log(y + 1e-7)) / batch_size

1차원일때에는 reshape 를 통해 데이터의 형태를 바꿔준다.
레이블이 원-핫 인코딩이 아니라 ‘2’, ‘5’ 등으로 주어졌을 때에는 다음과 같이 구현 가능하다.

  def cross_entropy_error(y, t):
      if y.ndim == 1:
          t = t.reshape(1, t.size)
          y = y.reshape(1, y.size)
      batch_size = y.shape[0]
      return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

4.2.5 왜 손실 함수를 설정하는가

숫자 인식에서의 목표는 높은 ‘정확도’를 이끄는 매개변수를 찾는것이다.
- 그러면 정확도 지표를 사용하면 되는데 왜 굳이 손실 함수를 택하는 것일까?
신경망 학습에서의 ‘미분’의 역할에 주목한다면 답변이 된다.
- 최적의 매개변수를 탐색할 때 손실함수의 값을 가장 작게 하는 매개변수 값을 찾는데,
- 이때 매개변수의 미분(기울기)를 계싼하고, 그 미분값을 단서로 매개변수의 값을 점차 갱신하는 과정을 반복한다.
가중치 매개변수의 손실함수의 여기서 미분이란
- 가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실 함수가 어떻게 변하나
- 미분 값이 양수면 가중치 매개변수를 음의 방향으로, 음수면 양의 방향으로 변화시켜 값을 줄여나감.
정확도를 지표로 삼는다면, 미분 값이 대부분의 장소에서 0이 되어 매개변수를 갱신할 수 없다.
그럼 왜 정확도를 지표로 삼으면 미분 값이 0이 될까?
- 100장의 이미지 중 32장을 올바로 인식한다면 정확도는 32%이다.
  - 여기서 가중치 매개변수의 값을 조금 조정해도, 정확도는 여전히 32%일 것이다.
  - 미세한 변화에는 반응하지 않는다.(미분 값 0)
- 매개변수를 계속 조정해나가서 33장을 올바로 인식했다고 해보자.
  - 그러면 정확도는 33%가 되는데, 32%→33%→34%… 처럼 불연속적인 변화값을 보인다.
- 반면, 손실 함수의 값은 0.92543, 0.93432…. 등으로 연속적인 값으로 변화한다.
신경망에서 계단 함수가 아닌 시그모이드 함수를 활성화 함수로 사용하는 것도 같은 이유에서다.
- 계단 함수는 값이 급격히 변하는데 반해,
- 시그모이드 함수는 연속적인 값을 보이므로 기울기도 연속적으로 변한다.
  - 미분 값이 어느 장소라도 0이 되지 않는다.
결국, 기울기가 0이 되지 않는 성질 덕분에 신경망이 올바르게 학습할 수 있는 것

4.3 수치 미분

미분을 복습하자.
- 수치 미분이란, 진정한 미분값을 ‘근사치’로 계산하는 방법이다.
- 오차가 없이 진정한 값을 얻어내는 것은 해석적 미분 이라 한다.
  - 수학 시간에 배운다고 하는데, 나는 7차 교육 과정이라… 안 배웠음.

4.3.1 미분

10분에 2km씩 달렸다고 했을 때, 1분에 0.2km만큼의 속도로 뛰었다고 해석할 수 있다.
위의 예시는 사실 평균 속도를 구한것이며, 미분은 ‘특정 순간’의 변화량을 뜻한다.
- 10분이라는 시간을 가능한 한 줄여,
  - 직전 1분에 달린 거리,
  - 직전 1초에 달린 거리,
  - 직전 0.1초에 달린 거리…
  - 식으로 간격을 줄여서, 한 순간의 변화량 (어느 순간의 속도)을 얻는 것이다.
함수의 미분을 나타낸 식은
- $\frac{df(x)}{dx} = \lim_{h\to0}{\frac{f(x+h)-f(x)}{h}}$
  - 좌변은 $f(x)$의 $x$에 대한 미분 ($x$에 대한 $f(x)$의 변화량)을 나타내는 기호
  - $x$의 ‘작은 변화’가 함수 $f(x)$를 얼마나 변화시키느냐를 의미

파이썬에서 구현을 해보자.

  # 나쁜 구현 예
  def numerical_diff(f, x):
      h = 10e-50
      return (f(x+h) - f(x))/h

작은 값을 대입하고자 h를 사용했다.

위 코드는 개선할 점이 두 가지가 있다.
1. 10e-50는 반올림 오차 문제를 일으킨다.
```
 h = np.float32(1e-50)
 print(h)    # 0.0
```
  - 이 미세한 값 h로 1e-4를 이용하자. (좋은 결과를 얻는다고 알려짐)
2. 함수 $f$의 차분과 관련한 것.
  - 차분: 위 구현에서는 $x+h$와 $x$ 사이의 함수 $f$의 차분을 계산하고있지만, 애초에 이 계산에는 오차가 있다.
  - 진정한 미분은 $x$위치의 함수의 기울기 이지만, 이번 구현의 미분은 $x+h$와 $x$사이의 기울기에 해당한다.
    - ($h$를 무한히 0으로 좁히는 것이 불가능해 생기는 한계)
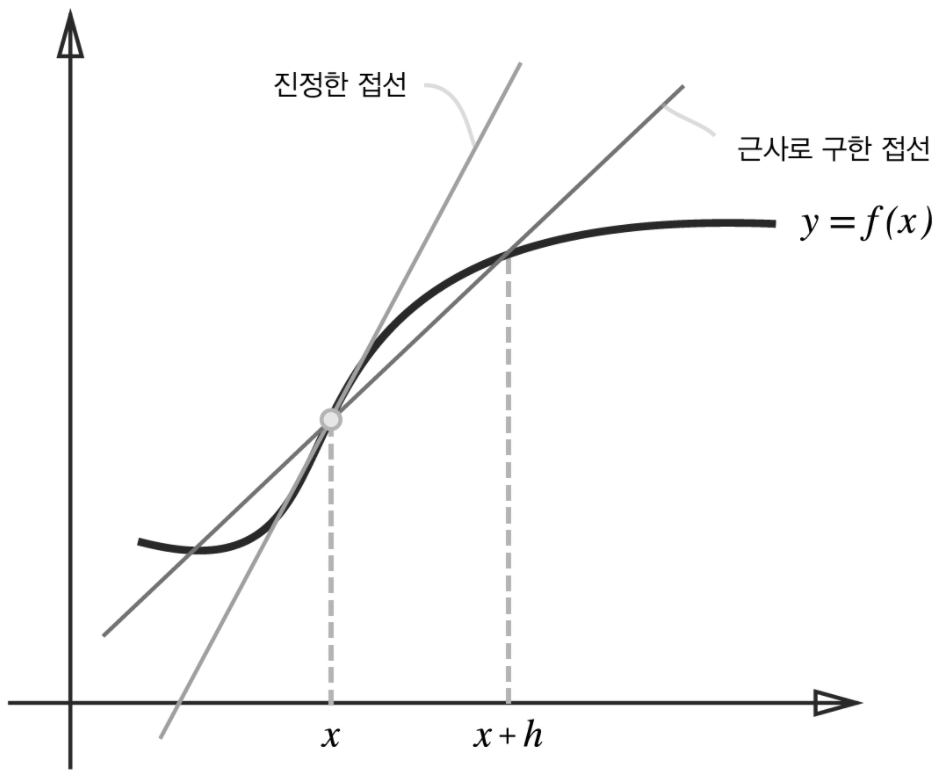
  - 이 오차를 줄이기 위해, $(x+h)$와 $(x-h)$일 때의 함수 $f$의 차분을 계산하는 방법을 쓰기도 함
    - $x$를 중심으로 그 전후의 차분을 계산한다는 의미에서 중심 차분, 중앙 차분이라 함
    - 위에서 언급한 $x$와 $(x+h)$의 차분은 전방 차분이라 함
```
 def numerical_diff(f, x):
     h = 1e-4 # 0.0001
     return (f(x+h) - f(x-h)) / (2*h)    # 중앙 차분
```

4.3.2 수치 미분의 예

수치 미분을 사용하여 간단한 함수를 미분해보자.
- $y=0.01x^2+0.1x$
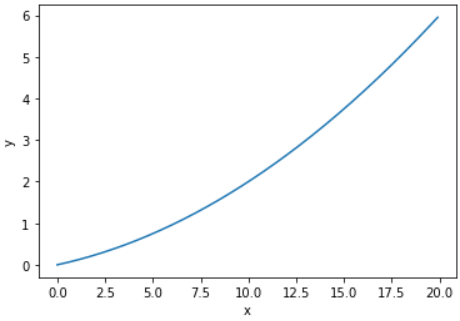
- $x=5$일 때와 $x=10$일 때 이 함수의 미분을 계산해보자.
```
  numerical_diff(function_1, 5)    # 0.1999999999990898
  numerical_diff(function_1, 10)    # 0.2999999999986347
```
  - 위의 값이 $x$에 대한 $f(x)$의 변화량이다. (함수의 기울기)
  - 또한, $f(x) = 0.01x^2+0.1x$의 해석적 해는
    - $\frac{df(x)}{dx}=0.02x+0.1$이다.
      - $x$가 5, 10일 때의 ‘진정한 미분’은 0.2, 0.3으로, 수치 미분 결과와의 오차가 매우 작다.

4.3.3 편미분

편미분이란, 변수가 여럿인 함수에 대한 미분을 뜻한다.
- 그래서 어느 변수에 대한 미분이냐에 대해 구별해야한다.
아래의 식을 살펴보자.
- $f(x_0, x_1) = x_0^2+x_1^2$
```
  def function_2(x):
      return np.sum(x**2)
```
- 위 식을 그리면 아래와 같다.
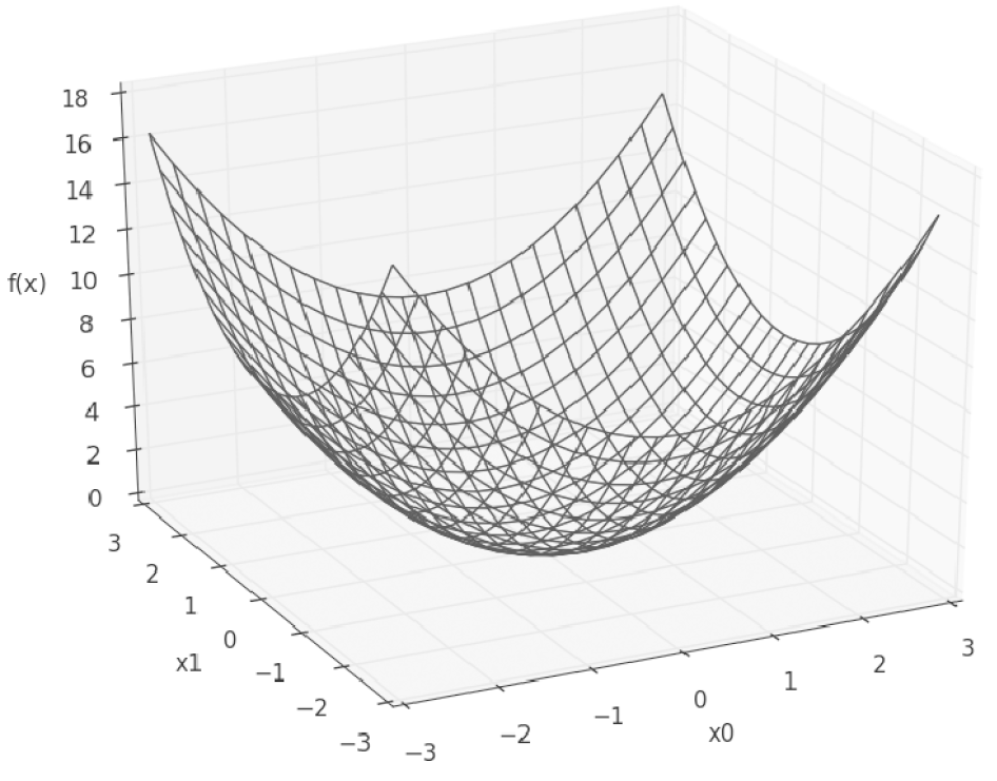
- 위 식에서 $x_0$와 $x_1$중 어느 변수에 대한 미분이냐를 구별해야하며,
  - 수식으로는 $\frac{\partial f}{\partial x_0}$이나 $\frac{\partial f}{\partial x_1}$처럼 쓴다.

그럼 편미분은 어떻게 구할까?

$x_0=3, x_1=4$일 때, $x_0$에 대한 편미분 $\frac{\partial f}{\partial x_0}$을 구해보자.

  def function_tmp1(x0):
      return x0**2 + 4.0**2

  numerical_diff(function_tmp1, 3.0)    # 6.00000000000378

$x_0=3, x_1=4$일 때, $x_1$에 대한 편미분 $\frac{\partial f}{\partial x_1}$을 구해보자.

  def function_tmp2(x1):
      return 3.0**2 + x1**2

  numerical_diff(function_tmp2, 4.0)    # 7.999999999999119

변수가 하나인 함수를 정의하고, 그 함수를 미분하여 풀어낸다.
- 이처럼 편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구한다.
- 다만, 여러 변수 중 목표가 되는 변수에만 초점을 맞추고 다른 변수는 상수로 고정한다.

4.4 기울기

앞에서는 $x_0$과 $x_1$의 편미분을 변수별로 따로 계산하였는데, 이를 동시에 계산하려면 어떻게 할까?

$x_0=3, x_1=4$일 때, $(x_0, x_1)$ 양쪽의 편미분을 모두 묶어 $(\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1})$처럼 모든 변수의 편미분을 벡터로 정리한 것을 기울기(gradient)라고 한다.

  def numerical_gradient(f, x):
      h = 1e-4
      grad = np.zeros_like(x)
      for idx in range(x,size):
          tmp_val = x[idx]
          # f(x+h) 계산
          x[idx] = tmp_val + h
          fxh1 = f(x)
          # f(x-h) 계산
          x[idx] = tmp_val - h
          fxh2 = f(x)

          grad[idx] = (fxh1-fhx2) / (2*h)
          x[idx] = tmp_val
      return grad

  numerical_gradient(function_2, np.array([3.0, 4.0]))    # array([6., 8.])

그럼 이 기울기가 의미하는 것이 무엇일까?
- $f(x_0, x_1) = x_0^2+x_1^2$의 기울기
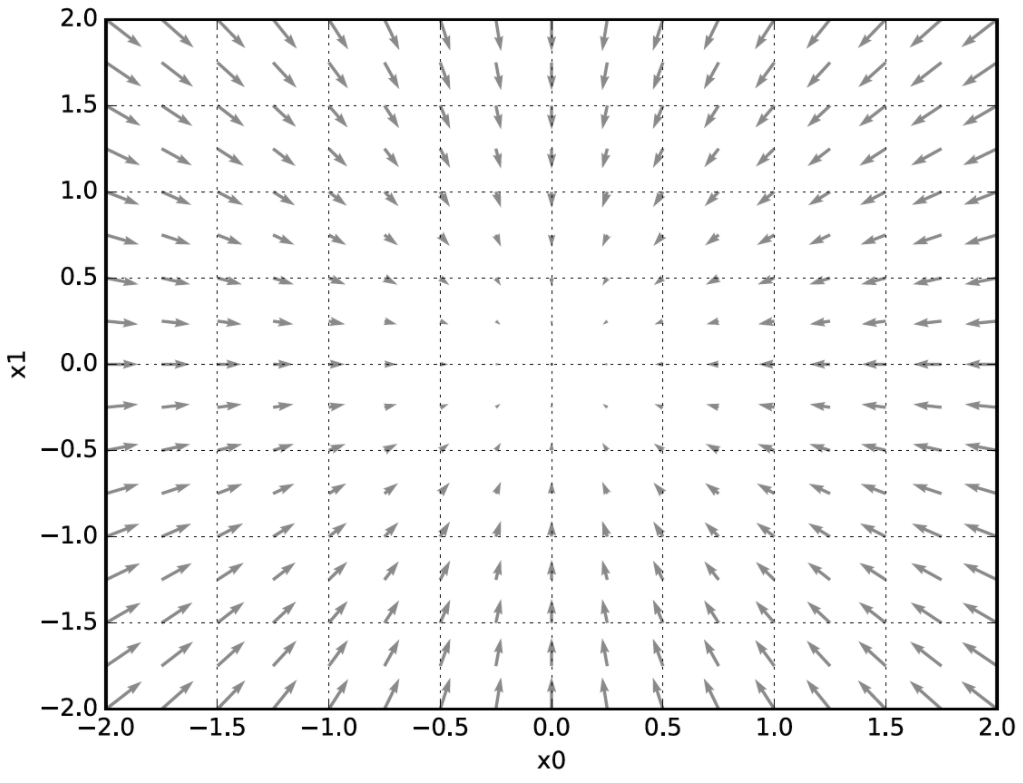
- 위 그림을 보면, 기울기는 함수의 ‘가장 낮은 장소(최솟값)’을 가리킨다.
- ‘가장 낮은 장소’에서 멀어질수록 화살표의 크기가 커진다.
  - 사실 그림에선 기울기가 가장 낮은 장소를 가르키지만, 실제로 반드시 그렇다고는 할 수 없다.
정확히 정리하면,
- 기울기가 가리키는 방향은 각 장소에서 함수의 출력 값을 가장 크게 줄이는 방향이다.

4.4.1 경사법(경사 하강법)

기계학습과 마찬가지로, 신경망도 최적의 매개변수를 학습 시 찾아야한다.
- 손실 함수가 최솟값이 될 때의 매개변수를 최적값이라 하는데, 일반적으로 손실 함수는 매우 복잡하다.
- 이 때 기울기를 이용하여 함수의 최솟값을 찾으려는 것이 경사법이다.
각 지점에서 함수의 값을 낮추는 방안을 제시하는 지표가 기울기이다.
- 다만, 그 기울기를 따라간다고 해서 무조건 최솟값을 찾을 수 있지는 않다.
- (global minimum, local minimum)
경사법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동한다.
- 도착한 곳에서도 마찬가지로 기울기를 구하고, 그 방향으로 나아가기를 반복한다.
- 위 방법으로 함수의 값을 점차 줄여나가는 것을 경사법(gradient method)이라고 한다.
  - 경사 하강법, 경사 상승법이 존재하지만, 방법론에는 큰 의미가 없고, 주로 경사 하강법으로 많이 등장한다.
이를 수식으로 나타내보자.
- $x_0 = x_0 - \eta \frac{\partial f}{\partial x_0}$
- $x_1 = x_1 - \eta \frac{\partial f}{\partial x_1}$
- $\eta$는 갱신하는 양을 나타내며, 학습률(learning rate)라고 한다.
  - 한 번의 학습으로 얼마나 학습해야 할지, 매개변수 값을 얼마나 갱신하냐를 정하는 것
- 위에서 변수가 늘어도, 같은 식(각 변수의 편미분 값)으로 갱신하게 된다.
학습률이 너무 크거나 작으면 제대로 학습할 수 없기 때문에, 값을 변경해가며 올바르게 학습하고 있는지 확인한다.

경사 하강법을 구현해보자.

  def gradient_descent(f, init_x, lr=0.01, step_num=100):
      x = init_x

      for i in range(step_num):
          grad = numerical_gradient(f, x)
          x -= lr*grad
      return x

경사 하강법으로 간단한 문제를 풀어보면,

$f(x_0, x_1) = x^2_0+x^2_1$의 최솟값 구하기

  def function_2(x):
      return x[0]**2 + x[1]**2

  init_x = np.array([-3.0, 4.0])
  gradient_descent(function_2, init_x, lr=0.1)    
  # array([-6.11110793e-10,  8.14814391e-10])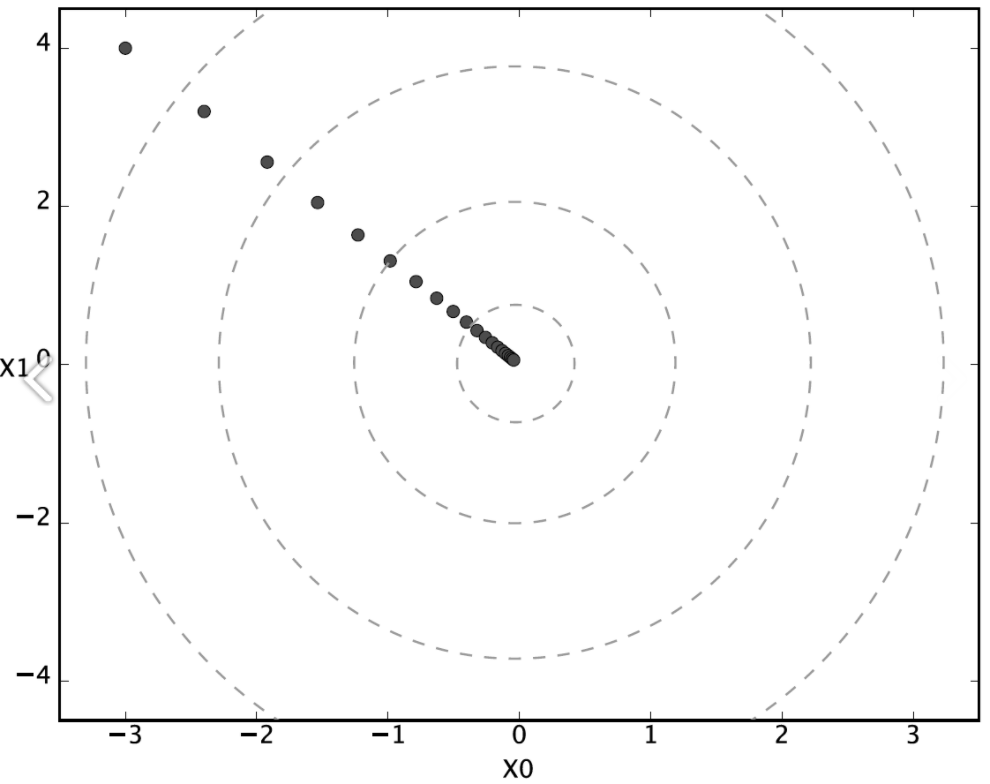

/assets/images/DLscratch/4//Untitled%205.png

(-3, 4)에서 시작하여 점차 값이 가장 낮은 장소로 가까워지고있다.

그럼 학습률을 크거나 작게 하면 어떻게 될까?

  gradient_descent(function_2, init_x=init_x, lr=10, step_num=100)    
  # array([-2.58983747e+13, -1.29524862e+12])

  gradient_descent(function_2, init_x=init_x, lr=0.001, step_num=100)    
  # array([-2.45570041,  3.27426722])

학습률이 크면 큰 값으로 발산하고, 작으면 갱신이 거의 되지 않고 끝나버린다.

학습률과 같은 매개변수를 하이퍼파라미터라고 한다.
- 가중치, 편향 같은 매개변수와는 성질이 다른 매개변수이다.
- 가중치 매개변수는 알고리즘에 의해 자동으로 획득되는 매개변수임에 반해,
- 하이퍼파라미터는 사람이 직접 입력해주어야한다. 그리고 최적값을 찾아야함.

4.4.2 신경망에서의 기울기

신경망에서의 기울기는 가중치 매개변수에 대한 손실 함수의 기울기를 뜻한다.
- 예를 들어, 가중치가 $\bf{W}$, 손실 함수가 $L$인 신경망이 있다면,
- 경사는 $\frac{\partial{L}}{\partial{\bf{W}}}$로 나타낼 수 있다.
  - 경사 행렬의 각 원소는 각각의 원소에 관한 편미분이며,
  - $w_{11}$을 조금 변경했을 때 $L$이 얼마나 변화하느냐를 나타낸다.
- $\bf{W}$와 $\frac{\partial{L}}{\partial{\bf{W}}}$의 형상은 동일하다.

f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
dW

'''
array([[ 0.07867118, -0.11764071,  0.03896953],
       [ 0.11800678, -0.17646106,  0.05845429]])
'''

자세한 코드는 생략하고, 경사 행렬을 살펴보자.
- 배열의 (1,1)은 약 0.07로, $w_{11}$를 $h$만큼 증가시키면 0.07만큼 손실 함수가 증가한다는 뜻이다.
- (1,2)는 약 -0.11로, $w_{12}$를 $h$만큼 증가시키면 -0.11만큼 손실 함수가 감소한다는 뜻이다.
- 손실 함수를 줄인다는 관점에서는, $\frac{\partial L}{\partial \bf{W}}$의 값 중 양수 값은 음의 방향으로, 음수 값은 양의 방향으로 갱신하면 된다.
- 또한, 갱신되는 양에는 $\frac{\partial L}{\partial \bf{W}}$의 절대값으로 기여하므로, $w_{11}$보다 $w_{12}$가 더 크게 기여한다.
신경망의 기울기를 구한 다음에는 경사법에 따라 가중치 매개변수를 갱신하기만 하면 된다.

4.5 학습 알고리즘 구현하기

신경망 학습의 절차를 정리해보자.
1. 미니배치
  - 훈련 데이터를 무작위로 가져옴, 이 미니배치의 손실 함수 값을 줄이는 것이 목표
2. 기울기 산출
  - 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기 구함.
  - 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시
3. 매개변수 갱신
  - 가중치 매개변수를 기울기 방향으로 갱신
4. 1~3단계를 반복
미니배치로 무작위로 데이터를 선정하기 떄문에, 확률적 경사 하강법(stochastic gradient descent, SDG) 이라고 부른다.

요약

기계학습에선 훈련, 테스트 세트로 나눠서 사용
신경망 학습은 손실 함수를 지표로, 손실 함수 값이 작아지는 방향으로 가중치 매개변수를 갱신
갱신 시, 가중치 매개변수의 기울기를 이용, 기울어진 방향으로 가중치의 값을 갱신, 반복
수치 미분을 이용해 가중치 매개변수의 기울기를 구함

서울숲 미세먼지