신경망 학습 관련 기술들을 살펴보자.

6. 학습 관련 기술들

• 머신러닝에서도 학습을 위해 그리드서치, 파이프라인 등과 같은 하이퍼 파라미터값을 조정하는 기술들이 존재한다.
• 딥러닝에서의 최적화 관련 기술들을 살펴보자.

6.1 매개변수 갱신

• 신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는것이다.
  • 이는 매개변수의 최적값을 찾는것이며, 이것을 최적화(optimization)라고 한다.
• 앞장에서 살펴본 SGD를 포함한 다양한 방법들을 살펴보자.

6.1.1 확률적 경사 하강법(SGD)

• (복습)SGD를 수식으로 표현하면 다음과 같다.
  • $\mathbf{W}\leftarrow \mathbf{W}-\eta \frac{\partial L}{\partial \mathbf{W}}$
    • $\mathbf{W}$: 갱신할 가중치 매개변수
    • $\eta$: 학습률 (0.01, 0.001 etc…)
    • $\frac{\partial L}{\partial \mathbf{W}}$: $\mathbf{W}$에 대한 손실 함수의 기울기
    • 결국 위 식은, 기울어진 방향으로 일정 양만큼만 가겠다!라는 뜻

6.1.2 SGD의 단점

• SGD는 단순하고 구현도 쉽지만, 문제에 따라 비효율적인 경우가 있다.
  • 비등방성(anisotropy)함수에서는 탐색 경로가 비효율적이다.
    • 비등방성 함수: 방향에 따라 성질(기울기)이 달라지는 함수
• 이런 단점을 개선해주는 방법을 알아보자.

6.1.3 모멘텀

• 모멘텀(Momentum)은 운동량을 뜻하는 단어로, 물리와 관계가 있다. 수식을 살펴보자.
  • $\mathbf{v} \leftarrow a \mathbf{v}- \eta \frac{\partial L}{\partial \mathbf{W}}$
  • $\mathbf{W} \leftarrow \mathbf{W}+\mathbf{v}$
    • $\mathbf{v}$는 물리에서 말하는 속도(velocity)에 해당한다.
    • 기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙을 나타낸 것인데,
    • 모멘텀은 공이 그릇의 바닥을 구르는 듯한 움직임을 보여준다.
  • SGD보다 지그재그의 움직임이 줄어든다. (학습이 빠르다.)

6.1.4 AdaGrad

• 신경망 학습에서는 학습률이 너무 작으면 시간이 오래걸리고, 크면 발산한다.
  • 그래서 학습률이 신경망 학습에서는 매우 중요하다.
• 이 학습률을 정하는 기술로 학습률 감소(learning rate decay)가 있는데,
  • 이는 학습을 진행하면서 학습률을 점차 줄여나가는 방법이다.
    • 처음에는 크게 학습, 점차 조금씩 학습
• 이를 간단하게 구현하면 매개변수 ‘전체’의 학습률 값을 일괄적으로 낮추는 방법이 있는데,
• 이를 발전시킨것이 AdaGrad 이다.
  • 각각의 매개변수에 맞춤형 값들을 만들어준다.
• 수식으로 살펴보자.
  • $\mathbf{h} \leftarrow \mathbf{h}+\frac{\partial L}{\partial \mathbf{W}} \odot \frac{\partial L}{\partial \mathbf{W}}$
  • $\mathbf{W} \leftarrow \mathbf{W} - \eta \frac{1}{\sqrt{\mathbf{h}}}\frac{\partial L}{\partial \mathbf{W}}$
    • $\mathbf{h}$: 기울기값을 제곱하여 계속 더해줌
    • 매개변수의 원소 중 많이 움직인 원소는 학습률이 낮아짐
• 갱신을 해갈수록 $\frac{1}{\sqrt{\mathbf{h}}}$값이 0에 수렴하므로 갱신 강도가 약해짐.
  • 이 이슈를 해결한 RMSProp이 존재함.
  • 모든 기울기를 계속 더하는 것이 아니라, 오래된 기울기는 서서히 잊고, 새로운 기울기 정보를 크게 반영하는 것.
  • 이 방법을 지수이동평균(Exponential Moving Average, EMA)이라고 함.

6.1.5 Adam

• 모멘텀은 공이 그릇 바닥을 구르는 듯한 움직임을, AdaGrad는 매개변수의 원소마다 다르게 갱신했다.
• 이 두가지 방법을 융합한 것이 Adam이다.
  • 학습률은 줄여나가되, 속도를 계산하여 학습의 갱신 강도를 갱신해나가는 것.

6.1.7 어느 갱신 방법을 이용할 것인가?

• 위에선 SGD, 모멘텀, AdaGrad, Adam 네 가지 방법을 살펴봤다.

• 이 네 기법의 결과를 비교해보자.

  

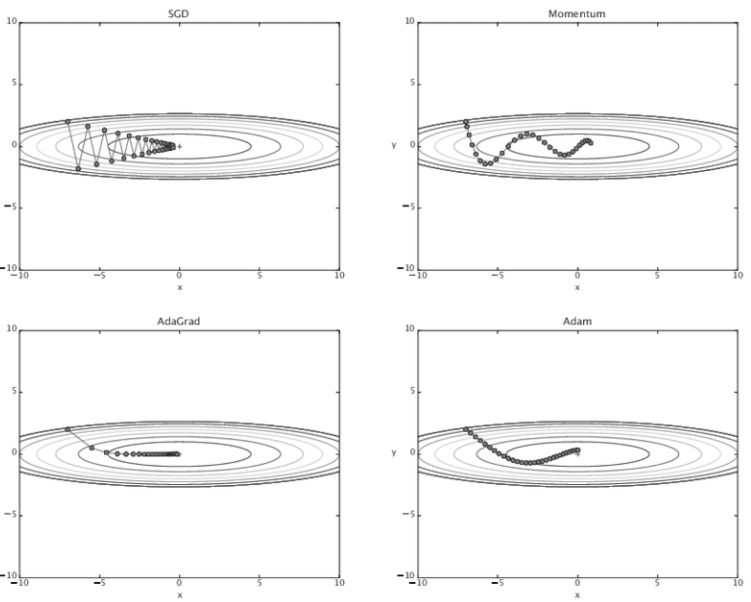
  • 각자 학습하는 방법이 다른 것을 알 수 있다.
• 명확하게 어떤것이 정답이다! 라는것은 없고, 문제에 맞게 옵티마이저를 설정한다고 한다.
  • 여전히 SGD도 많이 쓰고, 최근엔 Adam도 많이 쓴다고 한다.

6.2 가중치의 초깃값

• 신겨망 학습에서는 가중치를 어떻게 초기화시키는지도 중요하다.
• 실제로 가중치 초깃값을 무엇으로 하느냐가 성패를 좌우할 때도 있는데, 이번에는 이 초깃값에 대해 알아보자.

6.2.1 초깃값을 모두 0으로 하면?

• 오버피팅을 억제하여 일반화 성능을 높이는 기술인 가중치 감소(weight decay)를 살펴보자.
  • 가중치 감소란, 가중치 매개변수의 값이 작아지도록 학습하는 방법
• 가중치를 작게 만들고싶으면, 처음부터 모두 0으로 설정하면 안될까?
  • 모두 같은 값으로 시작하면, 오차역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문에 균일한 값으로 설정하면 안 된다. (가중치를 여러개 갖는 의미가 사라짐)
  • (곱셈 노드의 역전파 참고)
• 이렇게 가중치가 고르게 되어버리는 상황을 방지하려면, 초깃값을 무작위로 설정해야한다.

6.2.2 은닉층의 활성화값 분포

• 은닉층의 활성화값이 가중치 초깃값에 따라 어떻게 달라지는지 살펴보자.
• 활성화함수로 시그모이드함수를 사용한 5층 신경망에서의 활성화값(활성화함수의 출력값)을 살펴보자.

  • 초깃값이 표준편차가 1인 정규분포일 때,

    

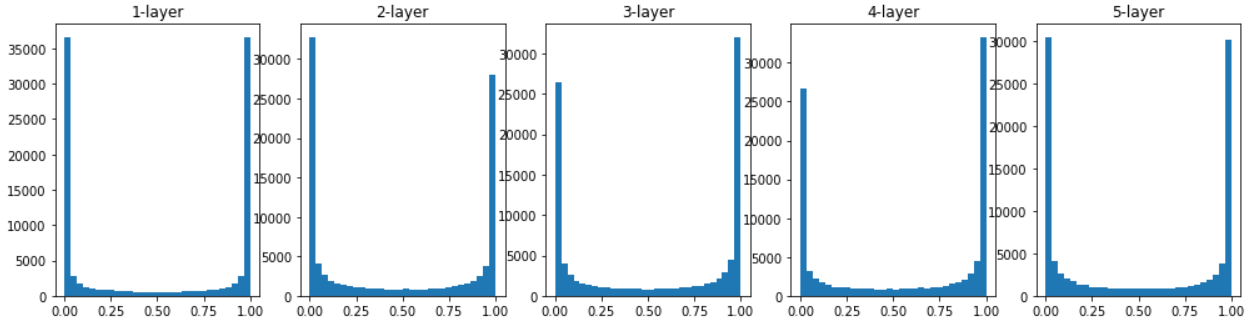
    • 0과 1로 모이는 현상을 보인다.
    • 시그모이드함수에서 0, 1에 가까워질수록 그 미분값은 0에 가까워지는데,
      • 이것이 기울기 소실(gradient vanishing)이라고 알려진 문제이다.

  • 이번에는 표준편차가 0.01일 때를 살펴보자.

    

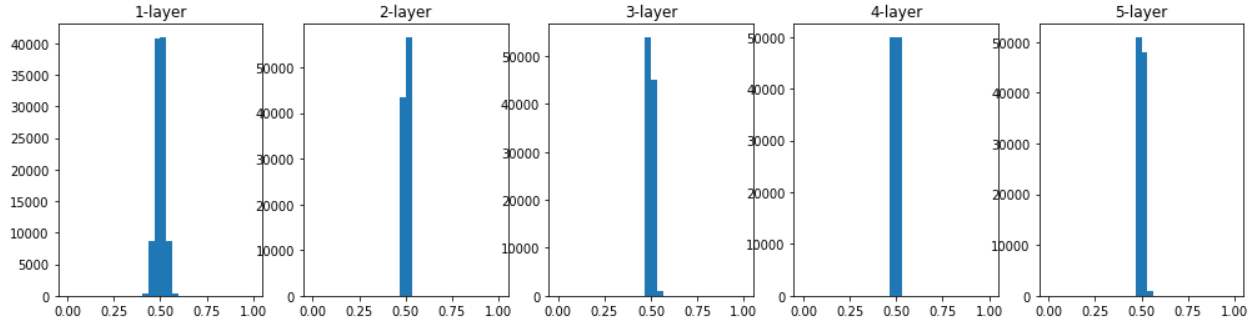
    • 활성화값이 치우쳐서 표현력을 제한한다는 문제가 발생했다.

  • 각 층의 활성화값은 적당히 고루 분포되어야한다. 층과 층 사이에 다양한 데이터가 흘러야 학습이 잘 되기 때문이다.

  • 이번에는 Xavier(사비에르) 초깃값을 써보자.

    • Xavier 초깃값은 노드가 $n$개일 때, 표준편차가 $\frac{1}{\sqrt{n}}$인 분포를 사용한다.

    

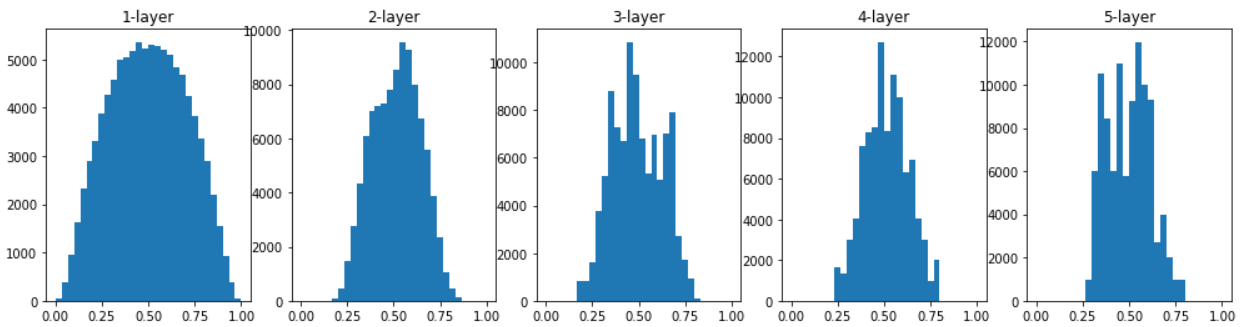
    • 확실히 위의 예보다는 분포가 안정된 것을 알 수 있다.
    • 다만, 층이 깊어질수록 모양이 일그러지는데, 이는 sigmoid 대신 tanh 함수를 이용하면 개선된다.
      • tanh함수는 sigmoid와 다르게 원점에서 대칭인 S 곡선 (sigmoid는 (0, 0.5)에서 대칭)

6.2.3 ReLU를 사용할 때의 가중치 초깃값

• Xavier 초깃값은 활성화 함수가 선형인 것을 전제로 이끈다.
  • Sigmoid, tanh 함수는 모두 S자 모양의 곡선 함수이지만 대칭점을 좌우로 하는 중앙 부분이 선형인 함수로 볼 수 있다.
• 반면 ReLU를 이용할 때에는 그에 맞게 특화된 초깃값을 이용해야한다.
  • 이 특화된 초깃값은 He 초깃값이라 한다.
    • He 초깃값은, 노드가 $n$개일 때, 표준편차가 $\sqrt{\frac{2}{n}}$인 정규분포를 사용한다.
    • 직관적으로 이해해보면, ReLU는 음의 영역이 0이라서 더 넓게 분포시키기 위해 2배의 계수가 필요하다고 해석할 수 있다.

• 그럼, ReLU를 이용한 경우의 활성화값 분포를 살펴보자. -

  

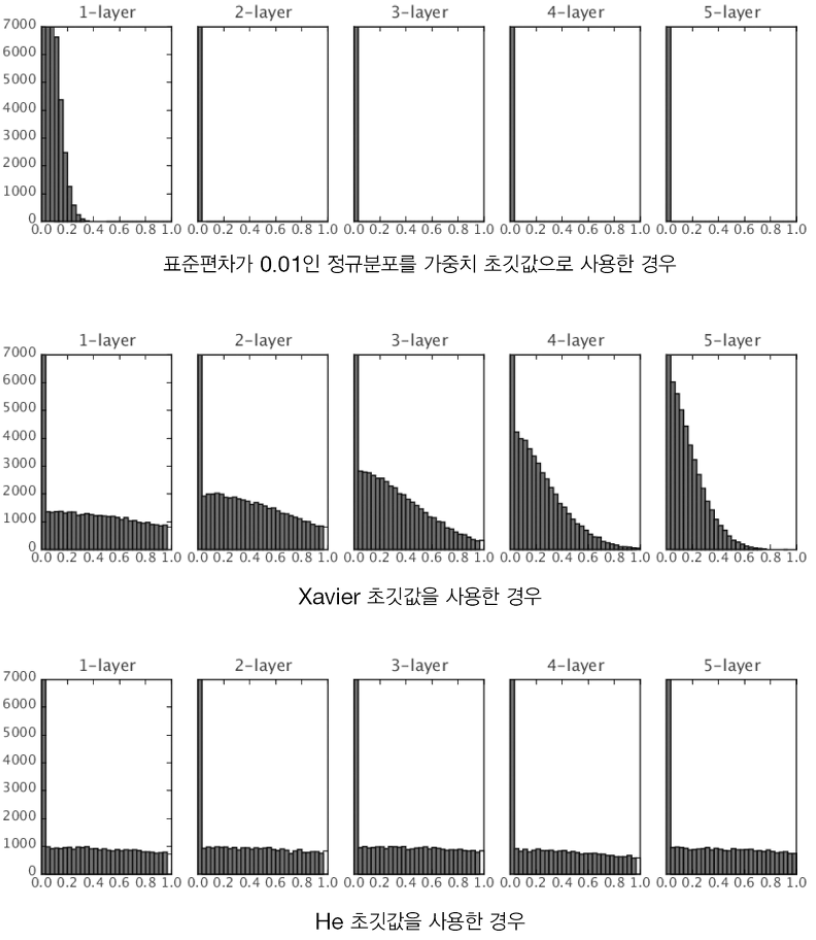
  • 확실히 He 초깃값을 쓰는 경우가 값들이 고루게 퍼짐을 확인해볼 수 있다.
    • Xavier 초깃값은 층이 깊어질수록 값이 치우쳐지며 기울기 소실 문제를 일으킨다.
• 정리하면,
  • 활성화 함수로 ReLU를 사용할 때는 He 초깃값을,
  • sigmoid, tanh 등의 S자 곡선일 때는 Xavier 초깃값을 사용한다.

6.3 배치 정규화

• 앞에서는 가중치의 초깃값을 적절하게 설정하여 각 층의 활성화값 분포가 적당히 퍼질 수 있도록 했다. 이를 통해 학습이 원활하게 수행됨을 확인했다.
• 배치 정규화(Batch Normalization)는 각 층이 활성화를 적당히 퍼트리도록 강제하는 아이디어에서 출발했다.

6.3.1 배치 정규화 알고리즘

• 배치 정규화가 주목받는 이유
  1. 학습 속도 개선
  2. 초깃값에 의존하지 않음
  3. 오버피팅을 억제함 (드롭아웃 등의 필요성 감소)
• 배치 정규화는 학습 시 미니배치를 단위로 정규화한다.
  • 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화.
  • 이 처리를 활성화 함수의 앞(혹은 뒤)에 삽입하여 데이터 분포가 덜 치우치게 할 수 있다.

6.4 바른 학습을 위해

• 오버피팅을 어떻게 해결할 수 있는지 살펴보자.

6.4.1 오버피팅

• 오버피팅은 주로 두 경우에 발생한다.
  1. 매개변수가 많고 표현력이 높은 모델(복잡한 모델)
  2. 훈련 데이터가 적음
• 오버피팅을 해결할 수 있는 방법들에 대해 살펴보자.

6.4.2 가중치 감소(weight decay)

• 학습 중 큰 가중치에 대해서는 큰 페널티를 부과하여 오버피팅을 억제하는 방법
  • 손실 함수의 가중치의 L2 노름을 손실 함수에 더한다.
  • 만약 가중치가 $\mathbf{W}$라 하면, L2노름에 따른 가중치 감소는 $\frac{1}{2}\lambda\mathbf{W}^2$가 되며, 이 값을 손실함수에 더한다.
    • $\lambda$(람다): 정규화의 세기를 조절하는 하이퍼파라미터
    • $\frac{1}{2}$: $\frac{1}{2}\lambda\mathbf{W}^2$의 미분 결과인 $\lambda\mathbf{W}$를 조정하는 역할의 상수
  • 이 계산을 통해, 가중치가 클 경우엔 벌점을 그만큼 크게 주며 오버피팅을 방지할 수 있다.

6.4.3 드롭아웃(dropout)

• 뉴런을 임의로 삭제하면서 학습하는 방법
  • 훈련 시마다 임의의 뉴런들을 삭제하여 학습시킨다.
  • 사실상 매번 다른 모델을 학습시키는것인데, 이는 머신러닝의 앙상블과 매우 유사하다.
  • 시험 때에는 각 뉴런의 출력에 훈련 때 삭제를 하지 않은 비율을 곱하여 출력한다.

6.5 적절한 하이퍼파라미터 값 찾기

• 신경망에서는 다양한 하이퍼파라미터들이 등장한다.
  • 당연히 이 값들을 어떻게 조정하냐에 따라 모델의 성능이 달라지는데, 적절한 하이퍼파라미터 값을 찾는 방법을 알아보자.

6.5.1 검증 데이터

• 머신러닝에서와 동일하게, 훈련세트에서 적절한 하이퍼파라미터 값을 찾기 위핸 검증세트를 따로 분리한다.
  • 결국 데이터셋을 세가지로 나누게 된다.
    • train set: 매개변수 학습
    • validation set: 하이퍼파라미터 성능 평가
    • test set: 일반화 성능 평가
  • 그럼 검증 세트(validation set)를 사용하여 하이퍼파라미터를 최적화하는 기법을 살펴보자.

6.5.2 하이퍼파라미터 최적화

• 최적화의 핵심은, 하이퍼파라미터의 ‘최적 값’이 존재하는 범위를 조금씩 줄여간다는 것
  • 대략적인 범위를 먼저 설정하고, 그 범위에서 무작위로 값을 골라낸 후(샘플링), 그 값으로 정확도를 평가.
    • 최종 정확도에 미치는 영향력이 하이퍼파라미터마다 다르기 때문에, 그리드 서치같은 규칙적 탐색보단 샘플링을 통한 무작위적 탐색이 더 효과적이라고 알려짐.
  • 따라서 하이퍼파라미터의 범위를 대략적으로 지정하는것이 효과적인데,
    • 주로 10의 거듭제곱 단위로 범위를 지정한다. (ex. 0.001부터 1000까지)
      • 이를 로그스케일이라고 한다.
• 최적화 시, 딥러닝 학습에는 오랜 시간이 걸린다.
  • 따라서 학습을 위한 에폭을 작게 하여, 1회 평가 시 걸리는 시간을 단축하는 것이 좋다.
• 지금까지의 과정을 정리해보자.
  1. 하이퍼파라미터 값의 범위를 설정
  2. 범위 내에서 무작위로 값을 샘플링
  3. 1단계에서 샘플링한 값을 사용하여 학습, 검증 데이터로 정확도 평가
  4. 1~2단계를 특정 횟수 반복 후, 그 정확도를 보고 하이퍼파라미터의 범위를 좁힘
• 더 세련된 기법은 베이즈 최적화를 살펴보자…

요약

• 옵티마이저로는 SGD, 모멘텀, AdaGrad, Adam 등이 있다.
• 가중치 초깃값을 정하는 방법은 학습 결과에 큰 영향을 끼치므로, 매우 중요하다.
• 가중치 초깃값으론 Xavier, He 초깃값이 효과적이다.
• 배치 정규화를 이용하면 학습을 빠르게 진행할 수 있으며, 초깃값의 영향에서 비교적 자유롭다.
• 오버피팅을 억제하는 정규화 기술로는 가중치 감소, 드롭아웃이 있다.
• 최적화 시 하이퍼파라미터 값 탐색은 범위를 점차 좁혀가며 하는 것이 효과적이다.