분류 알고리즘 - 분류의 지표는 무엇이 있을까?
업데이트:
3장. 분류
분류 알고리즘의 성능 지표들에 대한 내용이 주를 이룸
책 내용 중에서는 MNIST 데이터셋을 분류하는 내용이 자세히 나오지만, 이 포스트에서는 그 과정보단 분류의 지표에 대해서 주로 정리하였음
- 코드: 링크
목차
분류란
- 레이블이 범주 형식으로 구성되어있고, 새로운 레코드가 어떤 분류(레이블)에 속하는지 예측하는 문제
- [0, 1]과 같이 이진 분류가 있을 수 있고,
- [Kane, Son, Dele] 처럼 다중 분류가 있을 수 있다.
- 또한 하나의 레코드에 여러 레이블이 붙을 수도 있다.
- 예시로는, 사진 속 인물을 분류하는 문제인데, 한 사진에 여러 사람이 포함되어있는 문제
분류의 성능을 측정하는 방법
정확도(accuracy)
- 가장 간단하게는 실제값을 얼마나 잘 예측했는지 측정해볼 수 있다.
- 다만, 0인데 1로 예측한건지, 1을 제대로 예측한 비율은 얼마나 되는지에 대해 자세히 알 수 없다.
- 희소한 레이블이 존재한다면, 예를들어
- 0: 10,000개
- 1: 100개
- 모든 레이블을 0으로 예측하면 좋은 정확도가 나오지만, 실제로 좋은 모델은 아니다.
오차 행렬(confusion matrix)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train, y_train_pred)
-
실제 레이블을 어떻게 예측했는지 나타내주는 행렬
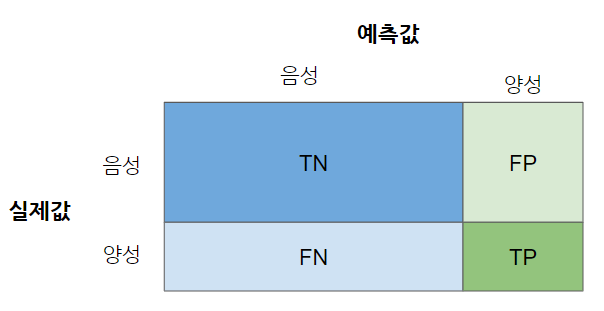
정밀도와 재현율
- 정밀도
- 양성으로 예측한 레이블 중 진짜 양성은 무엇인가?
- 수식: $\frac{TP}{TP+FP}$
- 예시: 어린 아이에게 좋은 자료를 전달해주는 분류기는 정밀도가 더 중요
- 재현율
- 진짜 양성 중, 실제로 양성으로 예측이라고 재현한 비율은?
- 수식: $\frac{TP}{TP+FN}$
- 예시: 범인 분류기는 재현율이 더 중요할 수 있음
- $F_1 score$
- 정밀도와 재현율을 한 지표로 나타낸 것
- 정밀도와 재현율의 조화평균
- 수식: $F_1 = \frac{2}{\frac{1}{정밀도}+\frac{1}{재현율}} = 2 * \frac{정밀도*재현율}{정밀도+재현율} = \frac{TP}{TP+\frac{FN+FP}{2}}$
- 정밀도와 재현율이 비슷한 상황에서는 $F_1$점수가 높지만, 이것이 항상 바람직한 것은 아님.
- 정밀도가 더 중요한 경우가 있고, 재현율이 더 중요한 경우가 있기 때문
- 정밀도와 재현율 트레이드오프
- 분류는 결정 함수를 통해 각 샘플을 분류하고, 그 임계값에 따라 정밀도와 재현율이 달라진다.
- 임계값이 정밀도와 재현율을 어떻게 나타내나 파악하고,
- 목표에 따라(정밀도냐 재현율이냐) 임계값을 정하는 것이 중요
ROC 곡선
- 거짓 양성 비율(FPR, False Positive rate)에 대한 진짜 양성 비율(TPR, True Positive rate)
- FPR
- 양성으로 잘못 분류된 음성 샘플의 비율
- 1-진짜음성비율(TNR, True Negative Rate)(=특이도)
- 재현율(민감도)에 대한 1-특이도 그래프
- AUC
- ROC곡선 아래 면적을 구한 것
- 완벽한 분류기는 AUC가 1, 완전 랜덤한 분류기는 0.5
정밀도-재현율과 ROC curve, AUC
- 두 곡선이 유사해서 언제 어떤 것을 쓸 지 헷갈리는데, 책에 설명이 나와있다.
- 일반적으로는,
- 양성 클래스가 드물거나, 거짓 음성보다 거짓 양성이 더 중요할 때 PR을 사용
- 그렇지 않다면 ROC, AUC 사용
- 결국 문제에 따라 달라짐.
다중 분류
- 이진 분류가 아닌, 둘 이상의 클래스를 분류하는 분류기
- 어떤 분류기를 써야하나?
- SGD, RF, Naive Bayes 등 일부 알고리즘은 직접 다중 분류가 가능하지만
- Logistic Regression, SVM 등의 알고리즘은 이진 분류만 가능
- 하지만, 이진 분류만 가능한 분류기를 여러개 사용하면 다중 분류 가능
- OvR(one-versus-the-rest) 혹은 OvA(one-versus-all)
- n개의 레이블이 있다면, 하나만 분류하는 분류기를 n개 만듬
- OvO(one-versus-one)
- 각 숫자의 조합마다 이진 분류를 훈련
- 레이블이 0~2일 때,
- 0과 1 구분
- 1과 2 구분
- 0과 2 구분
- 장점은, 전체 데이터로 훈련할 필요 없이, 각 모델에 두 레이블의 데이터만 있으면 된다는 점
- 하지만 대부분 OvR을 선호
에러 분석
- 단순히 지표만 보는 것이 아니라, 어느 레이블을 잘못 예측했는지 살펴보는 것도 중요.
- 특정 레이블에 레코드수가 편향되어있다면 비율로 에러를 확인하는 것도 좋은 방법
다중 레이블 분류
- 한 레코드에 여러 레이블로 분류
다중 출력 분류
- 다중 레이블 분류에서 한 레이블이 다중 클래스가 될 수 있도록 일반화한 것
- 값을 두 개 이상 가질 수 있음
댓글남기기