서울숲 미세먼지

서울숲 미세먼지

Product Data Analyst @Yogiyo

결정 트리 - 나누고 쪼개고 자르고 가르고

업데이트:

6장. 결정 트리

트리 모델에 대한 간단한 설명. 앙상블 모델을 위한 초석

결정 트리란

  • 목표 벡터를 예측하기 위해 트리구조로 부분집합을 만들어가는 과정

  • 사진으로 보면 쉽다.

    image

  • 분류 작업 예시 사진.

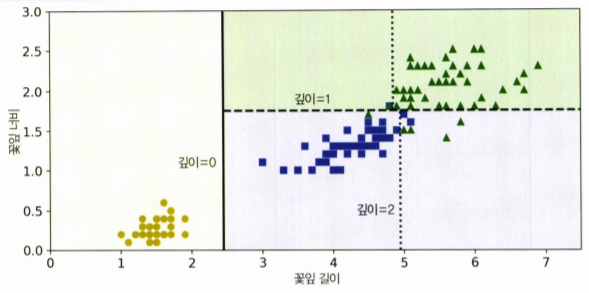
    image

  • 루트 노드에서부터 시작,
    • 특정 기준으로 특성들을 구분지어, 이진 트리의 형태로 데이터를 예측함.

결정 트리의 장단점

장점

  • 모델이 왜 그렇게 예측했는지 설명하기 쉽다. (이해하기 쉽다)
    • 특히 위처럼 시각화가 된다는 것이 큰 장점이지 싶다.
  • 데이터 스케일에 민감하지 않다.
  • 회귀와 분류 문제를 모두 풀 수 있다.

단점

  • 과대적합되기 쉽다.
    • 부분집합을 만들어가나며 (루트-리프-노드로 나뉘며) 영역을 작게 쪼개기때문에, 훈련 데이터에만 잘 들어맞을 수 있다.
    • 물론 하이퍼파라미터 조정하여 과대적합을 피할 수 있다.

  • 데이터의 변화, 회전에 민감하다.

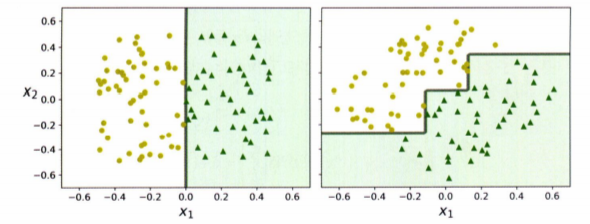
    image

    • 물론 PCA기법 등을 활용하면 해결할 수 있다.
    • 그리고 다음에 나올 배깅, 부스팅 등의 알고리즘으로 개선시킬 수 있다.

하이퍼 파라미터

  • 과대적합이 되기 쉬운만큼 조정할 매개변수도 많다.
  • 몇가지만 알아보자.
    1. min_samples_leaf
      • 분할을 위해 노드가 가져야 하는 최소 샘플의 개수
    2. min_samples_leaf
      • 리프 노드가 가지고 있어야 하는 최소 샘플 수
    3. max_leaf_nodes
      • 리프 노드의 최대 수
    4. max_features
      • 각 노드에서 분할에 사용할 특성의 최대 수
  • 꿀팁은 min~ 으로 시작하는 증가시켜서, max~ 는 감소시켜서 규제를 할 수 있다.

불순도

  • 불순도라는 개념이 나오는데, 노드에 몇 개의 클래스가 섞여있는지 나타내는 지표다.
    • 이를 gini점수로 수치화한다.
    • 한 노드에 [클래스0: 0개, 클래스1: 30개, 클래스2: 0개] 로 구성되어있으면 순수하다 라고 한다.(gini=0)
  • 지니 불순도?
    • 수식
      • $G_i = 1-\sum_{k=1}^{n}p_{i,k}^2$
    • $p_{i,k}$는 $i$번째 노드에 있는 훈련 샘플 중 클래스 k에 속한 샘플의 비율
    • [클래스0: 0개, 클래스1: 49개, 클래스2: 5개] 라면, 지니 점수는
      • $1-(0/54)^2-(49/54)^2-(5/54)^2\approx0.168$
  • 엔트로피(entropy)?
    • 규제를 지니가 아닌 엔트로피로도 지정하여 사용할 수 있음
    • 어떤 세트가 한 클래스의 샘플만 담고 있다면 엔트로피가 0
    • 수식
      • $H_i=-\sum_{\underset{p_{i,k}\neq0}k=1}^np_{i,k}\log_2\left(p_{i,k}\right)$
      • 수식 쓰는거 어렵다… $\LaTeX$…
    • [클래스0: 0개, 클래스1: 49개, 클래스2: 5개] 라면, 엔트로피는
      • $-\frac{49}{54}\log_2\left(\frac{49}{54}\right)-\frac{5}{54}\log_2\left(\frac{5}{54}\right)\approx0.445$
  • 언제 뭘 쓰나?
    • 실제로는 큰 차이가 없고, 비슷한 트리를 만든다.
    • 그리고 지니 불순도가 조금 더 계산이 빠르기에, 기본값으로 좋다.
    • 하지만 다른 트리가 만들어지는 경우엔,
      1. 지니 불순도
        • 가장 빈도 높은 클래스를 한쪽 가지(branch)로 고립시키는 경향 있음
      2. 엔트로피
        • 비교적 균형 잡힌 트리를 만들어냄

회귀

  • 분류와 매우 비슷하지만, 노드에서 클래스를 예측하는 것이 아닌, 값을 예측

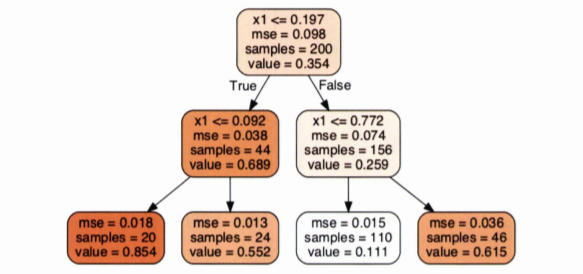
    image

    • 위 트리에서 $x_1=0.6$이라면 value=0.111인 리프 노드에 도달함
    • 이 때, 이 리프 노드에 있는 110개 훈련 샘플의 평균 타깃값이 예측값이 된다.

    • 이 예측값을 사용해 110개 샘플에 대한 MSE를 계산하면 0.015

      image

      • 분류와 마찬가지로, max_depth가 클 수록 train세트를 더 많이 훈련함
        • 과대적합 위험 상승
      • 각 영역의 예측값은 항상 그 영역에 있는 타깃값의 평균이 된다.
        • 예측값이 계단형태처럼 됨

  • 회귀에서 CART알고리즘은 불순도를 최소화하는 방향으로 분할하는 것이 아니라,

    • MSE를 최소화하도록 분할

CART 훈련 알고리즘

  • 결정 트리를 훈련시키기 위해서 사용하는 알고리즘
    • = 트리를 성장시키기 위해 사용하는
  • CART는 Classification And Regression Tree 의 줄임말인데,
    • 해석하면 분류와 회귀 트리를 훈련시키는 알고리즘이다… 영어로 쓰니까 있어보임.
  • 분류에 대한 CART 알고리즘은
    • 훈련 세트를 하나의 특성 $k$의 임계값 $t_k$를 사용해 두 개의 서브셋으로 나눈다.
      • ex. 꽃잎의 길이 ≤ 2.45cm
    • 가장 순수한 서브셋으로 나눌 수 있는 $(k, t_k)$짝을 찾아야하는데,
    • 이 알고리즘이 최소화해야하는 비용함수는 아래와 같다.
      • $J\left(k, t_k\right)=\frac{m_{\text{left}}}{m}G_{\text{left}} + \frac{m_{\text{right}}}{m}G_{\text{right}}$
      • $G_\text{left/right}$: 왼쪽/오른쪽 서브셋의 불순도
      • $m_\text{left/right}$: 왼쪽/오른쪽 서브셋의 샘플 수
    • 위 방식으로 훈련세트를 성공적으로 둘로 나누면, 같은 방식으로 계속 나누어나감
      • 설정한 규제에 다다르거나, 더 이상 불순도를 줄일 수 없을 때 멈춤
    • 회귀에서는 불순도G 대신 MSE로 계산

댓글남기기

참고